Tutorial 0: Finding your way around CurvedLand

Curved Space View

The blue circle at the center of the screen represents the curved space that you are occupying. The space illustrated by the CurvedLand applet is space of constant positive curvature; this is mathematically equivalent to the surface of a sphere. For more information about this model, click here.

For the purposes of analysis, we will always assume that you are at the North Pole on the surface of a sphere. The default for the applet is to show 90 degrees of the surface of the sphere in either direction; this means that you would be able to see all the way to the equator from the North Pole. You can adjust this visible angle by adjusting the slider labeled view size.

Shape Selection

Adjusting the view size will not do much until you have something drawn in your space. You can draw shapes in the space by selecting a type of shape using the radio buttons at the left side of the applet, and clicking and dragging in the space. You will notice that there are two types of shapes: true shapes and apparent shapes. True shapes are shapes defined according to the geometrical definitions in curved space; true lines are lines that follow great circles, or the geodesics in this type of space (to learn more about geodesics, read Tutorial 1), and true circles consist of all of the points equidistant from a center point. Apparent shapes are shapes that appear to be flat-space true shapes from your current perspective. The screen can be cleared of all of the shapes by pressing the erase button, or by pressing the center key on the numerical keypad when Num Lock is turned off.

Navigation Buttons

Navigation Controls

Trail Controls

Once you have drawn shapes, you can move around in the space and watch how those shapes start to distort from your perspective. To move, use the navigation arrows in the upper right-hand corner of the applet. It is also possible to move using the arrow keys on the keyboard, or the arrow keys on the numerical keypad (usually found on the right side of PC keyboards for desktop computers). In order to make the arrow keys on the numerical keypad work properly, ensure that Num Lock is turned off. Notice that you can also rotate using the buttons in the upper corners of the navigation button panel; another way to achieve rotation is by using the upper corner keys on the keyboard's numerical keypad. 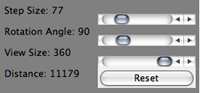To control the size of the steps you take each time you press a step button, adjust the step-size slider. You can also control the angle that you rotate through each time you press the rotate button by adjusting the rotation angle slider. In addition to this, the total distance you have traveled will be displayed on the right-hand side of the applet. You can reset this distance to 0 by pressing the reset button. You can also make a trail appear behind you showing where you have been; to do this, click the trail on button in the top left-hand corner of the applet. Next to this button is a clear trail button; this allows you to erase the trail (clear it from memory).

General relativity states that space-time is curved, yet we experience space-time as flat. When we draw a triangle, the angles add up to 180 degrees, and when we draw a circle, the ratio between circumference and diameter is pi. If we live in curved space-time, how can these things still be true? The key here is that, on a local level, curved space-time (or space) can be approximated by flat space-time; in other words, if you zoom in far enough, curved space looks flat. Try exploring this in the applet: zoom in to the smallest view size, and be sure to adjust the step-size slider as well so that steps remain inside the same view. Try drawing shapes and watching how they react as you move through the space. Compare this to how you expect shapes to change as you move through flat space.

Viewing 360 Degrees

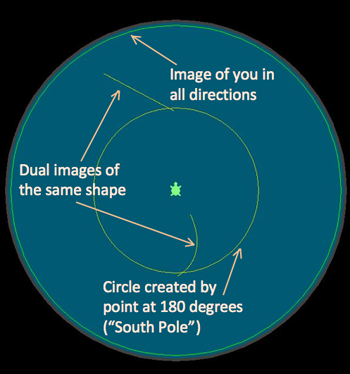
Next, try taking the view size to the other extreme. If you zoom all the way out by adjusting the view size slider so it is at its maximum value, the curvature of the space becomes very apparent (to move around, you may also want to increase the step size). The view size value should now be 360 degrees; this means that you can see 360 degrees around the sphere in either direction. Essentially, what you see in this view is all the way around the sphere and back to yourself. Turn the trail on; you should see a green circle that goes all the way around the edge of the visible space. This green circle represents you. If you were actually in this space, and you could see this far in every direction, then you would just see yourself.

Sight Lines on an Embedding Diagram

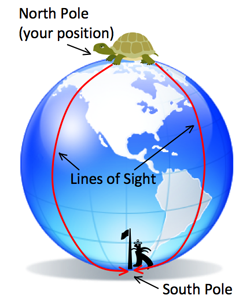
Think of yourself as being at the North Pole; if you draw a shape that crosses the South Pole then you will also see that shape in all directions (represented as a yellow circle at 180 degrees from the center). Draw some shapes in the space; each shape you draw should show up twice (although the two versions may look different from one another). This is because you will see each shape once before the South Pole, and once after the South Pole; if you think about your sight lines as rays reaching outward from the North Pole, those sight lines will first pass through all of the shapes on their way down to the South Pole, and then they will pass through all of the shapes again on their way back up to the North Pole (where you are).

To see this example in an even more extreme form, you can increase the maximum view size allowed by the slider and increase your view size to see even more of the space. To do this, click on the "Reset Maximum Zoom" button. Then enter a new maximum zoom value; it might be useful to start with multiples of 180 degrees. If you enter 720 degrees, and you adjust the view size to 720 using the slider, how images of each shape will you see? At what angles will you see yourself? At what angles will you see a spot at the South Pole? What if you increase your maximum view size to 1440 degrees?

A summary of the controls mentioned in this document is here. You can also display this summary inside the applet by clicking and dragging the bar at the bottom to expand it.

Copyright (C) 2010 Stephanie Erickson, Gary Felder
Terms and Conditions of Use