
I begin on Day 1 by writing this on the board:
3 + 7 = 7 + 3
This is called the "Commutative Property of Addition," but I have another word. I call it: obvious. If you have three apples and I have seven...or, if you have seven apples and I have three...the total we have together is the same either way, isn't it?
Now, I put something else on the board:
3 × 7 = 7 × 3
You can guess that this is the "Commutative Property of Multiplication." But I call it: not obvious.
Let's think about what that's saying. 3×7 means you have three groups, each of which has seven items. Let's count that out: 7, 14, 21.
7×3 means seven groups of three each. Let's count that out: 3, 6, 9, 12, 15, 18...21. Hey, it came out the same. It worked!
But is it just a coincidence? Will it also work for 6×9, and for 12×137, and for every other possible multiplication we could do? What I'm asking is, can you think of a reason that will make it obvious that these two things—three groups of seven, and seven groups of three—had to come out the same?
This is not a rhetorical question. I give the class some time to think about it, and I get a variety of answers. The simplest explanation I know is this picture:

Can you see it? You can look at this as three groups (rows) with seven squares each: 7+7+7. Or, you can look at it as seven groups (columns) with three squares each: 3+3+3+3+3+3+3. Either way, you get the same number of squares.
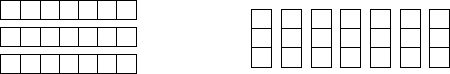
That picture convinces me that it will also work for 12×137: I don't have to count it out, and I don't have to take anyone's word for it either. It's...well, obvious.
So I'm not using the word "obvious" the way that most people do. When I say something is "obvious" I do not mean "anyone would figure it out quickly." Sometimes I spend hours and hours trying to make something obvious to myself. But if I succeed, I eventually get to the point where I can "Well, of course it's that way. It couldn't possibly be any other way." That, to me, is what math is all about.
Math is often compared to a foreign language. I've even heard math teachers say "math is just another language." I think this is a very misleading analogy.
Math has a language. Certain words ("root") are used very differently from how they are conventionally used, and other words ("polynomial") are never used outside of math. But these words express the math: they are not the math itself. If we started saying "fizbot" instead of root, the math ("you can't take the square fizbot of a negative number") would be the same.
What math has in common with a foreign language is that you have to memorize rules of how things fit together. "Je vais, tu vas, il va..." "Negative b plus or minus the square root of b-squared minus..." Apply these rules scrupulously or you will go in the wrong direction.
But here's the key difference. If you ask your French teacher "Why does it go Je vais, tu vas, il va?" the only answer you might expect is historical ("Here's how it evolved from the Latin roots"). You're not looking for "why it makes sense" because it isn't really supposed to. It's just how they talk in France.
In math, on the other hand, there is a reason why you can't take the square root of a negative number. There is a reason why 12÷4 is smaller than 12, but 12÷¼ is bigger than 12. And that reason has to go deeper than saying "When we divide by a fraction, we flip-and-multiply." It has to go to the heart of what division means, until you say "Well of course 12÷¼ has to be 48, and nothing but 48 would make sense. It's obvious!" (Hint: what does this problem mean in terms of pizza?)
To put it another way: if all the English speakers in the world decided tomorrow that we would use the word "thurple" to mean "lunch," they would all be correct—by definition they would be correct, simply because they agreed on it—and the world would go on just as before. But if all the mathematicians in the world decided that 37 was the same thing as 73, they would all, unanimously, be wrong. If they convinced the engineers, bridges would fall down. No one decided that there is no "Commutative Property of Exponents": someone figured it out. You can figure it out too.
So why don't people get that? Why do my students look terrified and cry out "Just tell us the answer!" when I suggest they figure something out?
For the most part, I blame their elementary school teachers. Very few people go into elementary school teaching because they love math. They go because they love children, they love playing games and telling stories, or (in some cases) it was the only professional job they could possibly get and keep (but that's a subject for another essay).
So the teacher learns the rules of math from the book, and teaches them from the book. And if a student asks "Why do we need a common denominator when we add fractions, but not when we multiply them," the teacher has no clue. Rather than risk embarrassment in front of the class, she glowers and says "Because that's how we do it."
It doesn't take long for the students to get the idea: don't try to think, just learn the rules. Or, to put it another way, all of math is glorified long division. We divide, multiply, subtract, bring down, divide, multiply, subtract, bring down, and some day when we're in high school we'll do pages and pages of dividing, multiplying, subtracting, bring downing.
Is it any wonder that they come out thinking math is pointless and boring?
In five years, my current crop of Algebra II students will not remember the laws of logarithms, and my Calculus students will not remember the quotient rule. I don't mind that a bit. If they ever need those things, they can look them up.
What I do hope they remember—and many of them have told me that they do—is that math is not at all what they used to think it was. Math is not a foreign language, or a set of rules that you learn and apply, or glorified long division. Math is the most perfect elaboration of common sense. It has no rules except the rules that we were all born with, built into our brains. And any time anyone tells you "This is the way it is" in math, you have the right—even the obligation—to ask why, and to keep asking why. You're not done when you can say "I can do it now." You're done when you say "Of course. Now that I see it this way...it's obvious."
COMMENTS
Would you say your particular use of the term "obvious" means "observable." In other words, 3+7 = 7+3 is obvious because you can picture the situation in your head (you have 3 apples, your friend has 7, or vice-versa). 3×7 = 7×3 is not obvious at first, because our minds aren't really programmed to hold enough data at one time to visualize even a simple multiplication. But the rectangle gives you a way of visualizing 3×7 = 7×3 and, viola, it's "obvious."
One final thought: I've noticed both your description of "obvious" and my comment rely quite a bit on language implying visions (i.e.: you "look" at the rectangle, "visualize" the rectangle, "observe" 3+7, etc.). The implication is that we need to "see" math in order for it to be obvious. This is another difference between math and a foreign (or domestic) language—in the latter you would ask whether a particular sentence "sounds" right.
I think you're raising a great point. The counter-argument would be, as anyone who has ever taken multivariate Calculus can assure you, that sometimes visualizing things properly is one of the most difficult and confusing parts of math. But, that being said, a huge amount of our brain is dedicated to visual processing. So as a general rule, I think that when we can make things more visual, we give our intuition a huge boost. I sometimes point out to my students that this is the only reason we bother graphing things: it never gives you information you didn't already have, but it allows you to lean on your brain's natural strength (visual pattern recognition) instead of its weakness (raw linear computation).
Well, in English the verbalizing of "I understand" is "I see." Same in Hebrew—"ani ro'eh"
Also in German "understanding properly" is Einsehen ("see inwards")
(while "It sounds right" is used to allow the possibility of some dubiousness)
This might not just be an habitual thing (as it often is, senselessly, in languages): The difference between sound and vision is in that the former deals with intake of sequential information whereas the latter is about simultaneous regard, and understanding is essentially about recognizing commonness of features, which can only be done if the compared elements are regarded simultaneously.
Thanks for your work—ponder?—there have been blind mathematicians—per search engines. A keen grasp of the obvious is, perchance, not entirely visual.
This was an awesome article. Thank you for writing. It's helped me immensely.
You said: "So the teacher learns the rules of math from the book, and teaches them from the book. And if a student asks 'Why do we need a common denominator when we add fractions, but not when we multiply them,' the teacher has no clue. Rather than risk embarrassment in front of the class, she glowers and says 'Because that's how we do it.'"
How does one go about figuring out and proving the reason why we need a common denominator when adding but not when multiplying? Like you said, "the teacher has no clue how to do it". So, how then, does someone like me in high school do it? This is something id like to understand! How do I play with this question and make it obvious to myself?
You said, "There is a reason why 12÷4 is smaller than 12, but 12÷¼ is bigger than 12."
I can see when I draw a pizza with 12 pieces, and divide each piece into 4 pieces itself, that each piece has four quarters. So there are 48 quarters in the 12 slices of pizza. Which is a bigger number. So a fraction divided into a whole number will always give a bigger number.
Is this how you go about making it obvious to yourself? Am I on the right track? Would you have done it another way?
You are absolutely on the right track. The very fact that you're thinking about these questions and trying to answer them, instead of memorizing algorithms, means you are 100% on the right track. In my experience, the #1 thing that distinguishes the "I-love-math-and-I'm-good-at-it" crowd from the "I-hate-math-and-can't-do-it" crowd is the habit of always asking these questions until everything makes sense. Once you've gotten past fractions (which is a superb place to start), think about all the other math you know. Why is a negative number times a negative number, a positive number? Why do we solve quadratic equations the way we do? Why are negative exponents defined in such a weird way? I don't know what level of math you're taking right now, but in Pre-Algebra, Algebra I, Geometry, Algebra II, PreCalculus, Calculus, and beyond, keep thinking this way. And do exactly what you did here—think it through the very best you can, on your own, and then ask someone else (such as a teacher, or me).
Enough philosophy. Let's get to your questions! First of all, let me say that fractions are all about pizza.
Let's start with the question 3/8 + 1/8. So, imagine a pizza that is cut in eight equal slices (which is a fairly common way to cut pizza, actually). Each slice is an "eighth." The fraction 3/8 simply means "three slices." So the question is, "If you have three slices, and I have one slice, how much do we have together?" So you put them together and you get four slices: 4/8.
That example demands two things of you, the reader.
You see what I mean? Convince yourself of one simple special case, then go quickly through a few other cases, and then see the general rule. We now know that it is very easy to add fractions, if they happen to have a common denominator.
Now, let's do a harder question: you have half a pizza, and I have a third. How much do we have together? This isn't easy if you cut the pizza the wrong way: say, into a half for you, a third for me, and a little leftover corner. But you can make it very easy if you cut the pizza into sixths! If you cut it that way, you can see clearly that your half a pizza is three slices, and my third of a pizza is two slices. So together, we have five slices: 5/6. You may recognize this as the old common-denominator trick, but when you approach it visually—don't just look at the words, draw the pizza!—you can see it in front of you. Once again, try another few examples, and then generalize.
Now, let's forget about addition and talk about division. "Why does dividing by a fraction make a number smaller?" is a question I get asked once in a while, and I know I embedded it in my essay, but it's really the wrong question. The right question is, "What does dividing by a fraction mean?"
So, let's start with whole numbers. What does 12 divided-by 3 mean? You might answer "I have 12 pizzas, and three friends. How much does each friend get?" That's a fine answer, but it breaks down when we introduce fractions. ("I have a fourth of a friend" is kind of a non-starter.) So let me try 12 divided-by 3 a different way. "I have 12 pizzas. I'm going to have a party, and each friend needs 3 pizzas. (Hey, they're small pizzas, OK?) How many friends can I invite?" The answer is still 4, of course. Take a moment to convince yourself that this is a very comfortable 12 divided-by 3 problem.
Because once you're there, you can do fractions. "I have 12 pizzas. I'm going to have a party, and each friend needs 1/4 of a pizza. How many friends can I invite?" It doesn't take long, from there, to convince yourself that the answer is 48. Try a few other examples, and then generalize. Without pizza, I can say in pure mathematical terms that a divided-by b means "How many of b does it take to make a?" How many 5s does it take to make 40? It takes 8. How many one-thirds does it take to make seven? It takes 21. You can still visualize this, but it's a bit more abstract now. It should make sense that dividing by a third is the same as multiplying by 3, and makes things bigger. And we're well on our way to the old "invert-and-multiply" rule for dividing fractions.
Whew! I'm sorry this message was so long. I get excited when people ask those questions. I hope it was helpful and not too boring!
Thanks for taking the time to write that! That's awesome! It was very helpful. I'm actually 26 years old, I've gone back to school and am studying high school level math in Australia (that's what i really meant by "I'm a high school student"). I want to understand the math im learning rather then just memorizing it. I'm just about to begin semester 2 and do calculus and advanced math. My teacher so far has avoided my "why" questions as best as possible. It's quite frustrating.
Back to that last email, you said:
More generally, you can see the rule "When two fractions have the same denominator, and you want to add them, you leave the denominator alone (don't add the two denominators!) but you add the two numerators."
This may be a silly question but...is this where the rule when adding numerators with a common denominator comes from? Is this how someone came up with that rule? Just the way you did it with a a couple of fractions and then generalized it? And then they basically said "it works every time so we'll tell the kids to just add the numerators and leave the denominators the same and put that in all the text books." Assuming no one ever figured out that rule before for adding fractions, could i have gone through that process and from that process alone created that rule? Or did they go further and write a proof or something first before they were like "yeh, that's the rule for adding fractions with a common denominator and it'll be true no matter what."
I guess what I'm also asking by asking this question is: is it good enough or the best way to learn the concepts of math (negative exponents, etc) in the way you described (visualize it and then generalize), or will there come a time where there is some shortcut or some kind of math logic i will learn we're i can write proofs out that make it clearer or something and let you see rules easier and why stuff works.
I suspect there is not, i suspect that visualizing it and then generalizing it and finding a pattern that is true in all cases is all that math really is. But maybe not? No one has ever really explained it to me. You don't know any books that give a birds eye view of math do you and how it all works?
I still haven't really got comfortable with what maths is and how people came up with all these rules and formulas. I've read about starting with simple statements or basic truths and then deriving everything else from there, but does that fit into what we're talking about. Or is what you described in your last email of just visualizing it and working it out until you understand it and then generalizing it what is considered to be "maths."
I should have guessed! It is so often the returning-to-school students who take things so much more seriously than the never-done-anything-else students. Sometimes I think we should send everyone out into the work force much earlier, and then let them come back to school if they want to. (really)
Anyway, you're asking some pretty philosophical questions, so you're going to have to indulge some pretty philosophical answers: look out! I want to say that you think you are asking one thing, but you are actually asking three very different questions with three very different answers.
The answer to question #1 is "I don't really know." You might be interested, just for fun, in picking up a book on the history of math. But I don't know a whole lot about it.
The answer to question #3 is "no." Real mathematicians approach these things like your old Geometry teacher did: here are the postulates, and here are the theorems that can be proven from these postulates. This approach gets very abstract. What exactly do we mean by "addition?" A real mathematician is completely unsatisfied with the answer "If I have 3 apples, and you have five apples..." He wants something formal, unambiguous, and generalizable. Starting with those formal definitions and a few postulates, he will eventually prove that (ax)/(bx)=a/b, and that a/x+b/x=(a+b)/x, and then you have the algorithm for adding fractions. Personally, I find I am more satisfied with a good hand-wave than with a formal proof, which is one reason I majored in Physics rather than math.
But now, question #2, which you expressed as: "Assuming no one ever figured out that rule before for adding fractions, could i have gone through that process and from that process alone created that rule?" The answer is yes, yes, yes! You're beginning to suspect, I think, that these rules actually do make sense, and that's the key. If someone in history had ever said "We're going to add fractions by adding the numerators and adding the denominators," he would simply be wrong. No matter how famous or important he was, he would still be wrong. A child could prove him wrong.
All that being said, I'm not saying that "see things specifically and then generalize" is the only approach you should ever use. There is definitely room for straight derivation. When people ask me why the laws of logs work the way they do, I usually answer by showing a simple pattern, but I can also answer by doing a little bit of algebra. And if you want to know why the quadratic formula works, you'll never get there by looking for patterns: you have to go through the algebra. But even there, the answer should not be "Because I said so."
As you head into Calculus, things are going to get much more abstract. You will need to be comfortable working through a fair bit of algebra, and you will need to be very comfortable with core algebra ideas such as functions. But most importantly, you need to never be satisfied with simply working the problem blindly and getting the right answer. If you memorize how to take a derivative, you have learned a not-very-amusing parlor trick. But if you really understand what a derivative means, then you have a solid foundation for higher math, or Physics, or engineering, or economics, or many other fields that rely on actually being able to use math.
 Kenny Felder's Essays and Commentaries:
Kenny Felder's Essays and Commentaries: www.felderbooks.com/kennyessays
www.felderbooks.com/papers