

Next: Scale Factor Evolution
Up: Field Equations and Coordinate
Previous: Field Equations
Selecting the Rescaling Variables
The program allows the user to set the rescaling variables 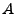 ,
, 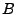 ,
,
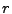 , and
, and 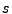 to whatever is most useful for a particular model (up to
one caveat discussed below). However there are certain guidelines that
we suggest following in setting these variables. These guidelines are
written into the program as defaults in the file
model.h. (See the section on how to implement new models for
more details on how the program sets these variables.) These default
settings are based on the following criteria:
to whatever is most useful for a particular model (up to
one caveat discussed below). However there are certain guidelines that
we suggest following in setting these variables. These guidelines are
written into the program as defaults in the file
model.h. (See the section on how to implement new models for
more details on how the program sets these variables.) These default
settings are based on the following criteria:
- We want to eliminate the first derivative term from the equation
of motion. This will make the equations simpler to solve.
- We want to set the scale of the field variables to be of order
unity, at least initially. This will make numerical calculations
simpler as well as making the output more readable.
- We want the coefficient of the dominant potential term to be of
order unity. This means the program time variable will automatically
measure the natural time scale of the problem.
- We want the coefficient of the dominant potential term to
include no powers of the scale factor. If this weren't true the time
scale of the calculations would be changing as the program progressed
and a fixed time step would be untenable.
The first two of these conditions immediately give us two
equations
 |
(6.7) |
and
 |
(6.8) |
where 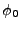 is the initial value of the inflaton (or whatever field
dominates initially). The latter two conditions require that we assume
some form for the dominant potential term. We assume that term to be
polynomial; if you wish to consider a model where the dominant term is
not polynomial you should expand it in a Taylor series and will
hopefully be able to identify an effective dominant polynomial
term. So take this dominant term to be of the form
is the initial value of the inflaton (or whatever field
dominates initially). The latter two conditions require that we assume
some form for the dominant potential term. We assume that term to be
polynomial; if you wish to consider a model where the dominant term is
not polynomial you should expand it in a Taylor series and will
hopefully be able to identify an effective dominant polynomial
term. So take this dominant term to be of the form
 |
(6.9) |
Then the corresponding term that appears in the equation of motion for
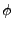 will be
will be
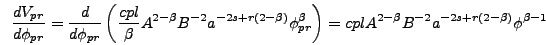 |
(6.10) |
so the last two criteria above give
 |
(6.11) |
 |
(6.12) |
Putting all these equations together
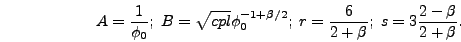 |
(6.13) |
If you choose to use these defaults you simply have to set 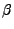 ,
,
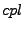 , and
, and 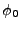 for your model and the other variables will be set
automatically according to equation
(6.13). Otherwise you can directly change the
definitions of
for your model and the other variables will be set
automatically according to equation
(6.13). Otherwise you can directly change the
definitions of 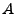 ,
, 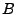 ,
, 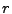 , and
, and 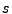 . All of these definitions are in
the file model.h. If you do explicitly change the four
rescaling parameters you should set the initial field values and
derivatives as needed for your rescaling scheme. (These values are all
set in the file parameters.h.) However, the relationship
. All of these definitions are in
the file model.h. If you do explicitly change the four
rescaling parameters you should set the initial field values and
derivatives as needed for your rescaling scheme. (These values are all
set in the file parameters.h.) However, the relationship
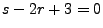 must be maintained because the evolution equations don't
include a first derivative term and will thus be invalid if this
relationship is violated. The variable definitions in model.h
explicitly set
must be maintained because the evolution equations don't
include a first derivative term and will thus be invalid if this
relationship is violated. The variable definitions in model.h
explicitly set 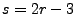 so you can independently set
so you can independently set  ,
,  , and
, and 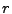 to whatever you wish.
to whatever you wish.
Using these default values the field equation becomes
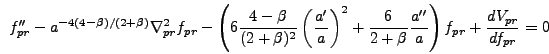 |
(6.14) |
where
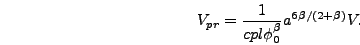 |
(6.15) |
Note that this expression for the potential will pick up additional
rescaling factors when 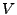 is expressed in terms of the program fields
is expressed in terms of the program fields
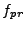 . For example a quartic coupling of the form
. For example a quartic coupling of the form
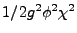 will give rise to
will give rise to
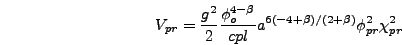 |
(6.16) |
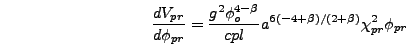 |
(6.17) |
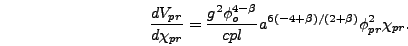 |
(6.18) |


Next: Scale Factor Evolution
Up: Field Equations and Coordinate
Previous: Field Equations
Go to The
LATTICEEASY Home Page
Go to Gary Felder's Home
Page
Send email to Gary Felder at gfelder@email.smith.edu
Send
email to Igor Tkachev at Igor.Tkachev@cern.ch
This
documentation was generated on 2008-01-21
![]() ,
, ![]() ,
,
![]() , and
, and ![]() to whatever is most useful for a particular model (up to
one caveat discussed below). However there are certain guidelines that
we suggest following in setting these variables. These guidelines are
written into the program as defaults in the file
model.h. (See the section on how to implement new models for
more details on how the program sets these variables.) These default
settings are based on the following criteria:
to whatever is most useful for a particular model (up to
one caveat discussed below). However there are certain guidelines that
we suggest following in setting these variables. These guidelines are
written into the program as defaults in the file
model.h. (See the section on how to implement new models for
more details on how the program sets these variables.) These default
settings are based on the following criteria:
![]() ,
,
![]() , and
, and ![]() for your model and the other variables will be set
automatically according to equation
(6.13). Otherwise you can directly change the
definitions of
for your model and the other variables will be set
automatically according to equation
(6.13). Otherwise you can directly change the
definitions of ![]() ,
, ![]() ,
, ![]() , and
, and ![]() . All of these definitions are in
the file model.h. If you do explicitly change the four
rescaling parameters you should set the initial field values and
derivatives as needed for your rescaling scheme. (These values are all
set in the file parameters.h.) However, the relationship
. All of these definitions are in
the file model.h. If you do explicitly change the four
rescaling parameters you should set the initial field values and
derivatives as needed for your rescaling scheme. (These values are all
set in the file parameters.h.) However, the relationship
![]() must be maintained because the evolution equations don't
include a first derivative term and will thus be invalid if this
relationship is violated. The variable definitions in model.h
explicitly set
must be maintained because the evolution equations don't
include a first derivative term and will thus be invalid if this
relationship is violated. The variable definitions in model.h
explicitly set ![]() so you can independently set
so you can independently set ![]() ,
, ![]() , and
, and ![]() to whatever you wish.
to whatever you wish.