

Next: Initial Conditions in One
Up: Initial Conditions on the
Previous: Initial Conditions for Field
Standing Waves: Preserving Isotropy
Equation (6.70) tells us the frequency of
oscillation of the mode 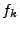 , but the question still remains
whether we should use the plus or minus sign in the exponential.
The answer is that we must use both. This fact arises from a
simple property of Fourier transforms, namely that the Fourier
transform of a real field
, but the question still remains
whether we should use the plus or minus sign in the exponential.
The answer is that we must use both. This fact arises from a
simple property of Fourier transforms, namely that the Fourier
transform of a real field 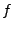 must obey the symmetry
must obey the symmetry
 |
(6.73) |
(It doesn't matter if you are considering a complex field since
you must still then set initial conditions for its real and
imaginary parts, and their Fourier transforms will be constrained
to obey this same symmetry relation.) We can ignore the expansion
of the universe for a moment and imagine that for some mode 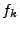 we have chosen to use the plus sign in the exponential, i.e.
we have chosen to use the plus sign in the exponential, i.e.
 |
(6.74) |
However, since both 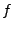 and
and 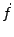 are real fields it must be
true that
are real fields it must be
true that
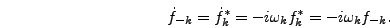 |
(6.75) |
In other words choosing the plus sign for a given momentum 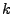 necessarily means using the minus sign for the momentum
necessarily means using the minus sign for the momentum 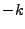 .
Recall that a mode
.
Recall that a mode 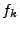 translates into a function
translates into a function 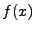 with
spatial dependence
with
spatial dependence 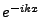 . So if you use the plus sign in
the exponential for some positive
. So if you use the plus sign in
the exponential for some positive 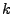 and the minus sign for
and the minus sign for 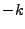 you have effectively initialized the two oscillatory modes
you have effectively initialized the two oscillatory modes
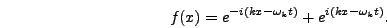 |
(6.76) |
In other words you have created a right moving wave. Likewise
choosing the minus sign in the exponential for a positive value of
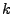 corresponds to setting up a left moving wave. Of course there
is no physically preferred direction on the lattice, so in reality
your initial conditions should contain equal components of right
and left moving fluctuations.
corresponds to setting up a left moving wave. Of course there
is no physically preferred direction on the lattice, so in reality
your initial conditions should contain equal components of right
and left moving fluctuations.
In practice the signs you use for the exponential time dependence
of different modes has a negligible effect on the evolution once
preheating begins. Even if every mode is initialized to be
left-moving, the total momentum this imparts to the field is
unnoticeable by the late stages of the evolution in every problem
we have considered. Nonetheless it is presumably desirable to
enforce Lorentz invariance, at least in an averaged sense. You
could do this by randomly initializing each mode with either a
plus or a minus sign. Instead, we choose to set up both left and
right moving waves with equal amplitude at each value of 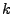 . In
other words the initial conditions correspond to standing waves.
Thus the final form of the initial fluctuations is
. In
other words the initial conditions correspond to standing waves.
Thus the final form of the initial fluctuations is
 |
(6.77) |
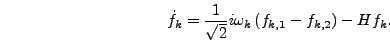 |
(6.78) |
where 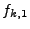 and
and 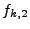 are two modes with separate random
phases but equal amplitudes determined by equation
(6.66).
are two modes with separate random
phases but equal amplitudes determined by equation
(6.66).
By now it may have struck you that we seem to be determining these
initial conditions based on issues of convenience, symmetry, and
so on. What about whatever is the physically correct form for
vacuum fluctuations, as given by their quantum mechanical
probability distributions? Shouldn't those distributions provide
an answer to all of these questions as to the correct form of the
equations? The answer is no. Although equation (6.65)
gives the correct quantum distribution for the mode amplitudes, it
is not correct to use this distribution and then use equation
(6.72) to set the values of the field derivatives. The
problem is that quantum mechanically 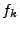 and
and 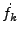 are
noncommuting operators and can not be simultaneously set. Although
this uncertainty presents a problem in principle it is unimportant
in practice. Once parametric resonance begins the occupation
numbers of the modes
are
noncommuting operators and can not be simultaneously set. Although
this uncertainty presents a problem in principle it is unimportant
in practice. Once parametric resonance begins the occupation
numbers of the modes 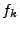 become large and their quantum
uncertainty becomes irrelevant. Moreover the rapid growth that
occurs during this resonance effectively destroys all information
about the initial values of the modes so that the final simulation
results are insensitive to the details of how the initial
conditions are set. In our experience runs that use the
probability distribution of equation (6.65) give
essentially the same results as ones that use the exact value of
equation (6.68) for each mode, and likewise all qualitative results are unchanged by the use of left-moving waves, right-moving waves, or any combination of the two.
become large and their quantum
uncertainty becomes irrelevant. Moreover the rapid growth that
occurs during this resonance effectively destroys all information
about the initial values of the modes so that the final simulation
results are insensitive to the details of how the initial
conditions are set. In our experience runs that use the
probability distribution of equation (6.65) give
essentially the same results as ones that use the exact value of
equation (6.68) for each mode, and likewise all qualitative results are unchanged by the use of left-moving waves, right-moving waves, or any combination of the two.


Next: Initial Conditions in One
Up: Initial Conditions on the
Previous: Initial Conditions for Field
Go to The
LATTICEEASY Home Page
Go to Gary Felder's Home
Page
Send email to Gary Felder at gfelder@email.smith.edu
Send
email to Igor Tkachev at Igor.Tkachev@cern.ch
This
documentation was generated on 2008-01-21
![]() , but the question still remains
whether we should use the plus or minus sign in the exponential.
The answer is that we must use both. This fact arises from a
simple property of Fourier transforms, namely that the Fourier
transform of a real field
, but the question still remains
whether we should use the plus or minus sign in the exponential.
The answer is that we must use both. This fact arises from a
simple property of Fourier transforms, namely that the Fourier
transform of a real field ![]() must obey the symmetry
must obey the symmetry
![]() . In
other words the initial conditions correspond to standing waves.
Thus the final form of the initial fluctuations is
. In
other words the initial conditions correspond to standing waves.
Thus the final form of the initial fluctuations is
![]() and
and ![]() are
noncommuting operators and can not be simultaneously set. Although
this uncertainty presents a problem in principle it is unimportant
in practice. Once parametric resonance begins the occupation
numbers of the modes
are
noncommuting operators and can not be simultaneously set. Although
this uncertainty presents a problem in principle it is unimportant
in practice. Once parametric resonance begins the occupation
numbers of the modes ![]() become large and their quantum
uncertainty becomes irrelevant. Moreover the rapid growth that
occurs during this resonance effectively destroys all information
about the initial values of the modes so that the final simulation
results are insensitive to the details of how the initial
conditions are set. In our experience runs that use the
probability distribution of equation (6.65) give
essentially the same results as ones that use the exact value of
equation (6.68) for each mode, and likewise all qualitative results are unchanged by the use of left-moving waves, right-moving waves, or any combination of the two.
become large and their quantum
uncertainty becomes irrelevant. Moreover the rapid growth that
occurs during this resonance effectively destroys all information
about the initial values of the modes so that the final simulation
results are insensitive to the details of how the initial
conditions are set. In our experience runs that use the
probability distribution of equation (6.65) give
essentially the same results as ones that use the exact value of
equation (6.68) for each mode, and likewise all qualitative results are unchanged by the use of left-moving waves, right-moving waves, or any combination of the two.