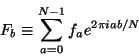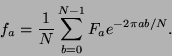Next: Output of Fourier Transforms
Up: Storage: What Goes Where
Previous: Storage: What Goes Where
The Fourier transform 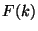 of a function
of a function 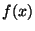 is defined as
is defined as
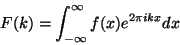 |
(1) |
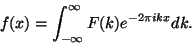 |
(2) |
A discrete Fourier transform takes a function 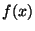 known only at
known only at 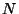 discrete points
discrete points
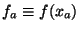 and gives back a function
and gives back a function 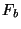 known only at the discrete points
known only at the discrete points 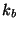
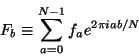 |
(3) |
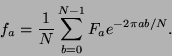 |
(4) |
Note that the relationship between the discrete Fourier transform and
the continuous one is
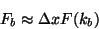 |
(5) |
where 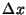 is the spacing between points
is the spacing between points 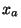 and the spacing
between frequencies
and the spacing
between frequencies 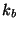 is given by
is given by
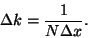 |
(6) |
(Note that I am following the conventions of Numerical Recipes using
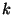 to denote frequency rather than angular frequency. The conversion
is simply
to denote frequency rather than angular frequency. The conversion
is simply
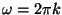 .) Formally the discrete Fourier transform
.) Formally the discrete Fourier transform
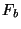 is periodic with period
is periodic with period 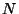 so
so 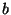 can take any set of
can take any set of 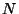 consecutive values. Practically speaking, though, if the points
consecutive values. Practically speaking, though, if the points 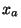 represent a typical region of the function
represent a typical region of the function 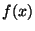 then the results
then the results
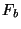 give the frequency components in the range
give the frequency components in the range
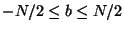 (where
(where
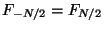 by periodicity). The next section
describes how these complex points are arranged in the output of the
routines fftc1 and fftcn. The following section describes the
additional information needed to interpret the results of the real
Fourier transform routines fftr1 and fftrn.
by periodicity). The next section
describes how these complex points are arranged in the output of the
routines fftc1 and fftcn. The following section describes the
additional information needed to interpret the results of the real
Fourier transform routines fftr1 and fftrn.



Next: Output of Fourier Transforms
Up: Storage: What Goes Where
Previous: Storage: What Goes Where
Go to The FFTEASY Home
Page
Go to Gary Felder's Home
Page
Send email to Gary at gfelder@email.smith.edu
This
documentation was generated on 2003-09-30
![]() of a function
of a function ![]() is defined as
is defined as