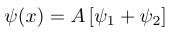
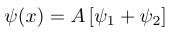
Active Reading Solution: Evolution of a Sum of Eigenstates

We begin in the following state: the wavefunction is the sum of two eigenstates, each with equal probabilities. Note that instead of ψ(x) this initial state could also be referred to as Ψ(x,0).

As the state evolves in time, each individual eigenstate is multiplied by a complex exponential. But they are different complex exponentials, each one based on its own eigenvalue E₁ or E₂.

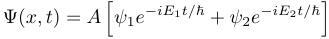
The position probability is based on the squared modulus of the wavefunction.

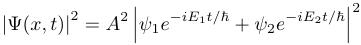
How do you find the squared modulus of a complex number? You multiply the number by its complex conjuate, which you generally write by replacing every occurence of i with -i.

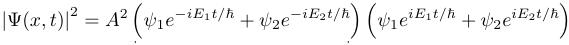
Multiply all that out.

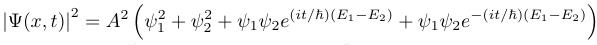
Remembering that e^ix = cos x + i sin x, we first expand out that first cross-term.

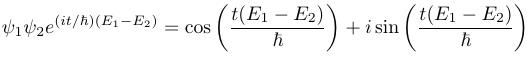
Now expand out the other cross-term. Then rewrite the result based on the fact that the cosine is an even function, and the sine is an odd function.

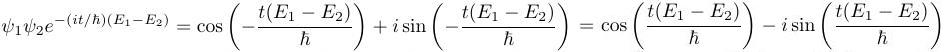
When we add those two cross-terms, the sines cancel out and the cosines add. That gives us our original goal, the modulus-squared of the time-evolved wavefunction.

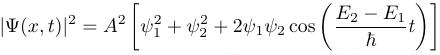
After all that, the real point is that the time dependence didn't cancel out, so the position probabilities are changing.