You almost certainly don't want to read this entire page from start to finish. I do recommend you start by reading the entire "The Basics" section. But after that, use the "Contents" menu at the top to jump to specific topics you need.
And by the way...if you are a high school math teacher, the good folks at NumWorks will give you a free calculator just to encourage you to try their product. I got mine that way, which led to the writing of this page. They also have an online simulator (free for anyone to download): it's useful for demonstrating the calculator to your class, and it's also how I got all the awesome screen shots in this Web page.
The yellow button above that, with a little picture of a house, takes you to the home menu.
Use the giant impossible-to-miss arrows to move up, down, left, and right.

Then hit either OK or EXE to choose an option. (Side note: I have not yet found any situation where OK and EXE work differently from each other. They seem to be the same button with two different names. Kinda weird.) Anyway, as an example, go to "Calculation" and hit OK if you want to enter equations and have the machine calculate things for you.
A few notes about the home screen.
If you go to "Settings" (one of the three menu options hidden below the top six in the home menu), you can change between radian and degree mode.
Don't stop reading now. You can't use the calculator until you learn how to enter equations!
Entering Equations
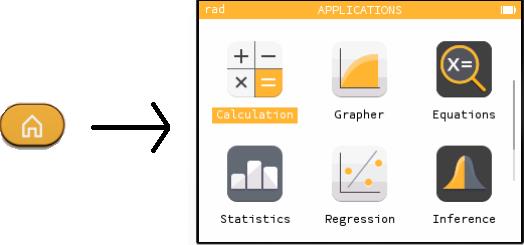
Choose "Calculation" from the home menu to get to a place where you can type equations. The picture below demonstrates some things that you might type.

On each line you see the question I typed (at the far left), and the answer the calculator gave (far right). For instance, when I asked for 4+3(-5) the calculator answered -11.
But there are a lot of details hiding in that little screen shot.
Help! I'm Stuck in a Fraction!
The picture below shows two different calculations that have two different answers.
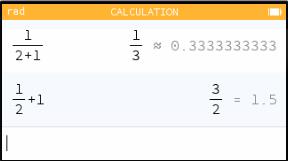
I hope it's clear that the calculator's answers are correct in both cases! But what I want to talk about is how I typed those.
If you type the following keys in the following order:
you get the first calculation I showed above, resulting in the answer 1/3. That's because the ÷ symbol creates a fraction and puts you in the denominator of that fraction. Then, as you keep typing, you're still in the denominator.
And that's great, if that's what you want. If not, the right-arrow key will get you out of the denominator. So the following key sequence produces the second equation above, the one with the answer 3/2.
It's confusing to follow what I'm saying here by just reading. To make it clear, type those two key sequences above on your calculator, and watch what happens at each step. You'll see how that right-arrow changes your cursor location so that the +1 ends up in a different place.
Similar considerations apply to square roots (such as the two different square root equations in the screen shot under Entering Equations above). And the same thing also happens with exponents that you create with the xy key (consider the difference between 53+1 and 53+1). However, the x2 key does not move the cursor up into the exponent, so you do not need to follow it with the right arrow.
This is all very different from the TI-83 that I was previously used to. (The TI-83 is much less visual, which causes a whole different set of problems.) But when I switched to the NumWorks, my equations kept coming out wrong. The problem was always this exact issue: I was still typing in the denominator of a fraction, or inside a square root, or up in an exponent, when I didn't mean to be.
At that point, I had to fix the equation that I had incorrectly typed (or was in the middle of incorrectly typing). Which brings me to...
Editing an Equation
Use the left and right arrows to move around within an equation that you are editing, just as you would on a computer. Use the backspace key (pictured below) to delete things. I used that backspace key a lot at the beginning, when equations didn't come out the way I meant them to, as described in Stuck in a Fraction above.
![]()
If you hit shift and then the backspace key, that clears out your current equation. (Note that the word clear is written on that key in yellow; more on that below.) Hit it again, and that clears out the whole screen.
That may all sound a bit obvious, but here's something that took me more by surprise: you can use the up-arrow to move up into the world of equations you have already entered. Navigate to an old answer or an old equation, and then hit EXE, and that equation will be copied to the bottom of the screen. Then you can mess with it—maybe change a 4 to a 5 or some such, moving around your equation with the arrows and the backspace key—before hitting EXE again to execute it. This is useful if you want to type an equation that is similar to, but not identical to, an equation you already entered.
For even more fun, notice that while you're arrowing around your old equations, many of them have a ... to the right. Click on that to get extra interesting information about that particular result: alternative answers, graphs, prime factorization, whatever the good folks at NumWorks could think of to throw in there.
Shift, Yellow, and Storing Numbers
A typical key on the calculator looks like this:
![]()
| Hit this key, and you get: | Hit the shift button and then this key: | Hit the alpha button and then this key: | Hit shift and then alpha and then this key: | |||
| cos (cosine) | acos (inverse cosine) | h | H |
OK, but what is h anyway? It is a named memory space. Using the ⟶ key (that's shift xy), you can put a number into memory h.
Here's an example. Suppose that, for some reason, the number 5×(π-2) keeps showing up in your calculations. (Hey, it could happen.) You need to add one to it, you need to double it, all kinds of things...and you don't want to keep typing it! So you type:
5×(π-2)⟶h
This performs the calculation you wanted, and then stores the result in the memory space called h. Thereafter, you can use h in calculations such as:
h+1
2h
1/h+6
...or whatever, you get the idea.
Every letter from a to z can hold its own number. And the capital letters A-Z are different memory spaces, giving you 52 in all.
A few ending notes about this feature.
Memory Clearing (The Cure-All)
You know how, if something goes wrong with your computer, you can sometimes fix it by turning the computer off and then back on again? Rebooting a calculator generally doesn't help, because it still remembers everything, including whatever is making it act funny right now. But what you can do, which should fix most mysterious problems, is clear out the memory.
Here's what you do. Go to "Settings" (by going to the home menu and then down-arrowing past the six options you can see to the three options you can't). All the way down at the bottom of the "Settings" menu is an option to "Reset the calculator." That should cure what ails you.
Here's an alternative approach. Look on the back of the calculator. (Make sure it isn't in its case!) In the middle you will see a tiny little hole labeled RESET. Poking into that hole will reset the memory. And here's the point: if you are a teacher who needs to reset 40 of these before a test, you can tell the students to put them on their desks face down, and then walk around and quickly reset them all with an unrolled paperclip.
* * *
At the very top of this page, I advised you to read through the entire "The Basics" section. If you've been reading from the top, congratulations—you have now done that! From here, rather than reading sequentially, I recommend you use the top menu to jump to whatever you need to learn.
To get you started, let's walk through a simple scenario.
![]()
If you're used to an ancient TI-83 like mine, you may suddenly feel like you have moved up in the world: these graphics are vastly better.
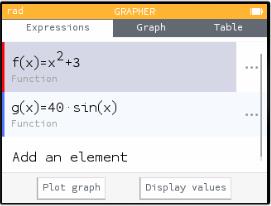
Now, let's say you want to graph more functions. Up-arrow to "Graph" (this may take several up-arrows). Then left-arrow to "Expressions" and hit EXE to go back where you were before, and do it all over again: choose "Add an Element" and add more functions. (You can see in the window below that I have two different functions listed. You can also see, by the way, that they are called f(x) and g(x). I never typed those names; I just typed x2+3 and 40sin(x).)
When you "Graph" you will see all of them side by side (just like on a TI-83), in different colors (so much nicer than a TI-83).
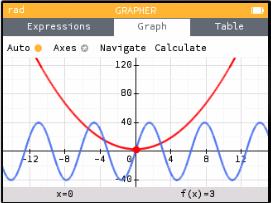
Protip: If you look closely at the pictures above, you'll see that in the "Expressions" tab (where I entered the equations), there is a red bar on the left of f(x) and a blue bar on the left of g(x). The calculator is associating each function with a color. You can see those colors in the graphs (in the picture above of the "Graph" tab), and you will see the same colors if you make a table of values.
The Graphing Window
In the example above, I asked the calculator to graph two functions: x2+3 and 40sin(x). As you can see in the picture, they are graphed in a window with x going from roughly -15 to 15, and y going from -40 to 120. I didn't choose any of that: the calculator uses fairly sophisticated algorithms that often give you a good window for your particular functions.
If you want to take tighter control, you can, although I'll admit I find this process a bit painful.
A Table of Values
Once you have entered one or more expressions, you can choose to look at a table of values instead of a graph. Arrow up to "Expressions," then right-arrow past "Graph" to where it says "Table" and (for the functions I entered above) you get the following.
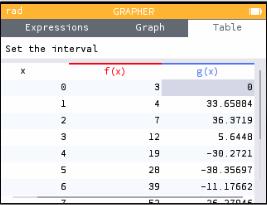
If you look carefully at that picture, you will see that above the table it says "Set the interval." You can arrow to that and hit EXE to set the starting x-value used in the table, and the step size between x-values.
Graphing in Polar Coordinates
You can graph a "polar" function r(θ) (as opposed to a "Cartesian" or "rectangular" function y(x), which is what I described above). I'll admit that I didn't find this process intuitive at first, but it's pretty efficient once you know what to do.
(As I was following my own directions, I noticed something that could be a bit confusing: I chose a template that said f(θ), but as soon as I hit EXE it became h(θ). That's because the calculator names functions sequentially, and I already had functions named f and g.)
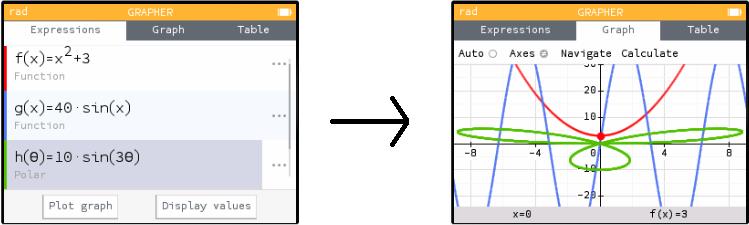
There's one more important feature here, which is that you can specify the domain of your function: that is, the θ-values that will be used in your graph. Here's how you do that.
In the "Expressions" tab, there is a ... to the right of each function. (You can see three of them in my picture above.) Right-arrow onto that ellipsis and hit EXE to get a little menu of options for that particular function. Here you can change the "Plot Restriction," setting the variables θmin and θmax.
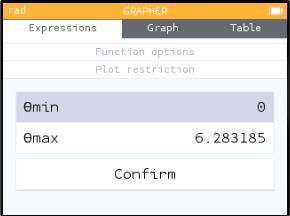
The drawing I showed above has θ going from 0 to 2π. If you (for instance) change θmax to π/2, you will only see part of that polar curve.

Comparison to the TI-83
On the TI-83, you switch into polar "mode." Then all your functions are r(θ) instead of y(x), and the "Window" includes a θmin and θmax. On the NumWorks you enter a polar function, but you don't switch into polar mode. This small-sounding difference allows you to do some things on the NumWorks that are not possible on the TI.
Graphing Parametric Equations
You can graph "parametric equations" x(t),y(t) (as opposed to a "Cartesian" or "rectangular" function y(x), which is what I described above). I'll admit that I didn't find this process intuitive at first, but it's pretty efficient once you know what to do.
(As I was following my own directions, I noticed something that could be a bit confusing: I chose a template that said f(t), but as soon as I hit EXE it became h(t). That's because the calculator names functions sequentially, and I already had functions named f and g.)
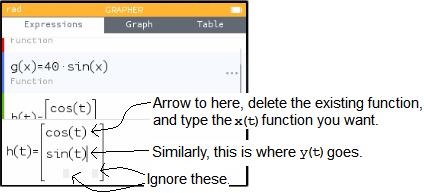
Edit the two functions that you see, leaving the other four little blank patches blank. The "x,n,t" button will give you a t in this equation.
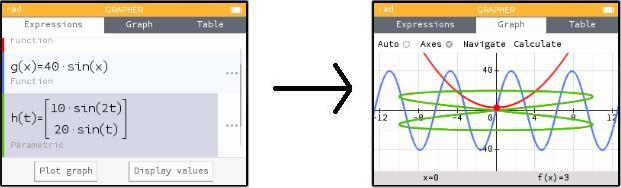
There's one more important feature here, which is that you can specify the domain of your function: that is, the t-values that will be used in your graph. Here's how you do that.
In the "Expressions" tab, there is a ... to the right of each function. (You can see two of them in my picture above.) Right-arrow onto that ellipsis and hit EXE to get a little menu of options for that particular function. Here you can change the "Plot Restriction," setting the variables Tmin and Tmax.
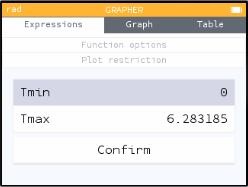
The drawing I showed above has t going from 0 to 2π. If you (for instance) change Tmax to π/2, you will only see part of that parametrically defined curve.

Comparison to the TI-83
On the TI-83, you switch into parametric "mode." Then all your functions are x(t),y(t) pairs instead of y(x), and the "Window" includes a tmin and tmax. On the NumWorks you enter a set of parametric equations, but you don't switch into parametric mode. This small-sounding difference allows you to do some things on the NumWorks that are not possible on the TI.
Curve Fitting, or Regression
"Regression" is a peculiar word that means you have a bunch of points, and you want to find a particular curve that most closely fits them. (For instance, you have done an experiment, and are now looking for the function that best models your data.)
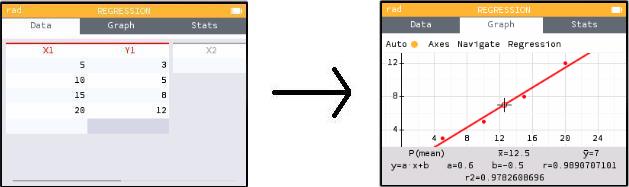
There's another important feature here that is not at all obvious. On the "Data" tab, up-arrow to where it says X1 (above your data but below the tab headings) and hit EXE. This brings you to a menu where you can clear out all the data in the column (which is certainly an important thing to be able to do). But this menu also has a submenu called "Regression" that gives you options besides linear regression. You can find the quadratic curve of best fit, exponential curve, logarithmic curve, and so on.

Here's a nifty alternative path. When you're looking at the graph of a function, up-arrow to where it says Auto, and then right-arrow to Calculate. Choose a function, and then toggle on the option "Value of the derivative." When you go back to the Graph, you will see f'(x) displayed at the bottom alongside x and f(x). Similarly, if you hit EXE on the f(x) at the top of a table column, you can switch on a derivative column in the table.
Important note: The calculator uses numerical approximation techniques to find derivatives. In some cases, those techniques will not work, and you will get an answer that is just plain wrong. Caveat emptor.
Definite Integrals
This calculator cannot tell you that the integral of 2x is x2+C. (Some more advanced calculators can.) But it can tell you that the integral of 2x evaluated between x=1 and x=4 is 15.

Important note: The calculator uses numerical approximation techniques to find integrals. In some cases, those techniques will not work, and you will get an answer that is just plain wrong. Caveat emptor.
Imaginary and Complex Numbers
If you ask the calculator for the square root of -1, it gives you an error. This is because the calculator defaults to "real" mode: there are no square roots of negative numbers.
If you are looking for a different answer, choose "Settings" from the home menu. (Can't find it? Go to the home menu and then scroll down, past the six options you see, to find the three other options you don't see.) Inside the Settings menu, go down to "Complex format" and choose "Cartesian."
Now go back and ask for the square root of -1 again, and this time you will get i.
Now that you are in this mode, you can do calculations with i. But look at the screen below. I asked the same-looking question twice—and I was in complex mode both times—but I got different answers. What happened?
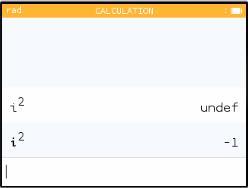
The sneaky answer is that there are two different "i"s (note in the screen shot the slightly different fonts). The first time I hit alpha and then the tan key. That gave me a variable called i, one of the 52 named variables spaces that you can use to store numbers. I hadn't stored anything in that space, so my answer was undefined.
The second time I used the actual i key (second row, next to the log). That is the imaginary number i, not a variable, and its square is -1.
Once you're in complex mode, hit the Toolbox button (pictured below—it's on the top row toward the right) and then go to the "Complex numbers" submenu to find operations such as magnitude and complex conjugate.
Series
A "series" means you're adding up a bunch of numbers.

In my example above, the NumWorks has just calculated that 32+42+52+62+72=135.
There are also options for working with sequences, including recursively defined sequences.
Matrices
I discussed earlier (under "Shift, Yellow, and Storing Numbers") the fact that the calculator has 52 named memory slots, each capable of holding a number. For instance, you can store the number 1.4 into the memory slot g and then use g in formulas.
The same memory slots can also hold matrices. Let's store one.
You know by know that hitting Shift before a key activates the function written in yellow on the key. What this key has in yellow is a left square bracket, indicating the opening of a matrix. The calculator gives you a blank 2×2 matrix to fill in.
Then hit EXE. Now your matrix is stored, associated with that letter.

The picture above stores a 3×3 matrix as the variable m.
And now what? You can find matrix operations by hitting the Toolbox button (pictured below—it's on the top row toward the right). That brings you to a menu: choose "Matrices and vectors" and then (under that) "Matrix," and you will find functions to find the inverse and the determinant of your matrix.
More interestingly, you can embed this variable in arbitrarily complicated equations. You will get errors if you do illegal matrix operations (such as taking the inverse of a non-square matrix, adding two matrices with different dimensions, etc). But as long as your matrices fit the operations, the calculator can do wonders. To take a few examples:
Factorial
Hit the Toolbox button (pictured below—it's on the top row toward the right). Then go to the "Probability" submenu, and then the "Combinatorics" sub-submenu, and factorial is in there.
Solving Equations
This feature—the ability to type an equation and have the calculator solve it for you—is the one that gets the most surprised and delighted reactions from my students.
The resulting screen, and its functionality, should be familiar if you've already done some function graphing. You're looking at a list of equations (although that list may currently be blank).
When you're typing an equation, you can get an equal sign by hitting shift π. Alternatively, just type a function with no equal sign; when you hit EXE the calculator will supply =0 as the end of your equation.
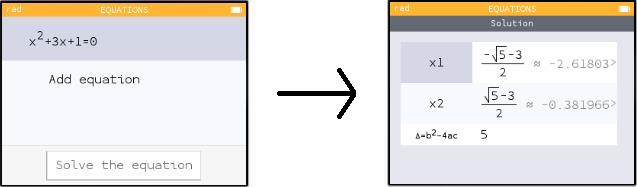
As you can see in my picture above, the calculator solves your equation and gives you one or more answers.

Comparison to the TI-83
The TI-83 offers similar functionality through its "Solver" (well hidden at the bottom of the Math menu). But one thing I always warn students about is that the TI Solver finds only one solution. You give it an x-value, and it hunts near that value until it finds a solution. If you want a different solution, you have to give it a different starting x-value.
By contrast, my picture above shows the NumWorks finding both roots of a quadratic function. I tried a cubic equation and it found all three. Then I tried cos x = x/20. This time the calculator asked me for minimum and maximum x-values. I told it to look between -20 and 20 (which is where all thirteen solutions are). It found ten of them, but warned me that there might be more.
I have no idea what the NumWorks is doing, or what are the limitations of its ability in this area, but it seems to be well out ahead of the TI.
But I have discussed all the functionality that I and my students need—enough to cover you up through BC Calculus. If you have something else you want to know, drop me an email at KenFe@HotMail.com and I'll reply to you and/or add it, if I know the answer!
 Gary and Kenny Felder's Math and Physics Help Home Page
Gary and Kenny Felder's Math and Physics Help Home Page
www.felderbooks.com/papers
 Send comments or questions to the author
Send comments or questions to the author