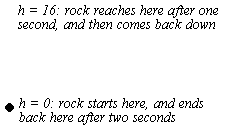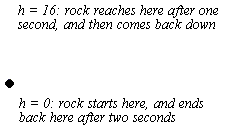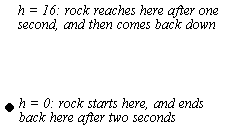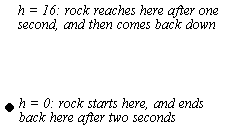Think Like a Physicist

So, the following experiment. I'm going to do an entire Physics lecture about math, but using no math at all. This may sound odd, or even useless, but I will make a very strong claim: the concepts in this small paper are exactly the concepts that prevent otherwise intelligent people from really enjoying Physics. Give this paper an hour of your life, and the payback—in terms of better grades, or just in terms of opening up a rich new mental world—could be absolutely enormous.

This paper is based on the following scenario: you throw a rock. It goes straight up into the air, and then comes down. That's all.

Now, let's put some numbers to it. First, let's assume that the rock starts at the ground (even though it would be difficult to throw a rock that way in real life). You throw the rock with an initial speed of 32 feet per second. It goes up for exactly one second, reaches a height of 16 feet, and then takes exactly one second to fall back down.

Finally, let's coin some letters. We will call the time t, measured in seconds. t starts at zero when the rock begins its journey, and reaches 2 at the end (because the whole trip is 2 seconds). We will call the height of the rock off the ground h, measured in feet. h starts at zero, when the rock is on the ground, goes all the way up to 16, and ends back at zero when the rock is back on the ground.
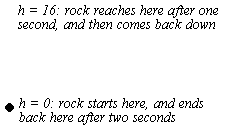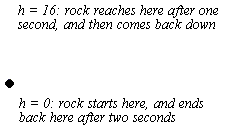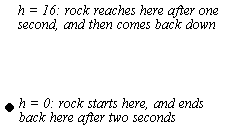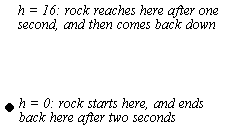(Wait a minute, I thought he said no math.)

(It's okay, those are just some numbers and letters. I promise not to try to add them or anything fancy like that.)
Okay, here comes the leap. At any given time t, the rock is at a certain height h. There is a mathematical equation that relates the two variables: that is, it tells you what h is, for any given time t. Let's call this the height equation. I'm not going to tell you what the height equation is (it's printed at the end, and you may already know it, but indulge me and don't use it). The key thing to know about this equation, is simply that it exists. And this whole paper is going to be a series of questions about what you would get, if you were to use this equation.

For each question, please read the question (in boldface) without looking at the answer (anything typed below the boldface). Then write down the answer you think is right, before you look at the real answer. Remember, do all of this without ever looking at, or using the equation!

Question 1: If you plug t=0 into the height equation, what h will you get?

In order to answer this question, you have to translate it into words. The word translation is: "what height is the rock at, after no time at all has elapsed?" I hope the answer is obvious by now: it is zero. At time t=0—at the beginning, in other words—the rock is on the ground, which means h=0. If you plugged t=0 and got any other value for h, that wouldn't mean your common sense was wrong. It would mean that the equation was wrong, or else you did your math wrong. That answer has to be right.

Question 2: If you plug t=1 into the height equation, what h will you get?

Question 3: If you plug t=2 into the height equation, what h will you get?

Question 4: If you plug t=3 into the height equation, what h will you get?

Your second guess might be that you will get 0. That's a pretty good guess! Because after three seconds, the rock will still be on the ground, at height zero.

But in fact, what you will discover if you do the math (*don't do it now, take my word for it!), is that you get a negative number. What does that mean?

What it means is that the equation is only valid during the time of the rock's flight: it doesn't know about the ground at all. The equation doesn't understand that the rock stops suddenly when it hits the ground. It blindly computes as if the rock was going to keep going, straight down, and hence finds a negative h. So in this case, the equation is just wrong! You know something about the problem that the equation doesn't know. So if you were asked "where will the rock be after three seconds?" you might use the equation: but when it gave you a negative number, you would have to be smart, and realize that it was lying to you. The right answer to that question is, "on the ground."

Question 5: If you plug h=16 into the height equation, what t will you get?

Question 6: If you plug h=0 into the height equation, what t will you get?

The answer is, it will say both. You will find both t=0 and t=2 come out of this one question.

Here I want to make a brief mathematical digression, which you can feel free to ignore if you like. h is a function of t. That means that for any given t there is exactly one h. But the reverse is not necessarily true. In principle, one h could have one t, or two, or none at all, or twenty. In this particular case, we will see 0, 1, or 2 answers, but never more. This might tip you off, if you remember your math, that a quadratic equation is at work. If it doesn't, that's okay too.

Question 7: If you plug h=10 into the height equation, what kind of values for t will you get? (ie how many answers; positive, negative, or zero?)

In this case, what you are asking the equation is: "when will the rock be at height 10?" The answer is, of course, twice: once on the way up, and once on the way down. So you would expect to get two answers back, both positive. One answer should be between 0 and 1 seconds, and the other should be between 1 and 2 seconds; since those represent the times that the rock was moving up and moving down, respectively. Going further, you might even recognize that the number 1 should be exactly in between the two numbers: so you might get 0.8 and 1.2, or 0.7 and 1.3, or something like that. But that is as far as you can go without crunching the math.

Question 8: If you plug h=20 into the height equation, what kind of values for t will you get? (ie how many answers; positive, negative, or zero?)

Question 9: If you plug h=-4 into the height equation, what kind of values for t will you get? (ie how many answers; positive, negative, or zero?)

But in fact, if you do the math, you will get two answers. Because the equation also doesn't know about the start of the rock's journey. So you will get one answer greater than 2, but you will also get a negative answer…signifying that the rock was below the ground, some time before we started counting!

Does that mean that the rock really started below the ground? No: once again, we know better than the equation. The rock was probably sitting on the ground, or maybe you were just putting it on the ground, or who knows what? before time t=0. But we know that we can't expect the equation to know that either.

Question 10: If you plug t=0 into the velocity equation, what kind of values for v will you get? (ie how many answers; positive, negative, or zero?)

Question 11: If you plug t=1½ into the velocity equation, what kind of values for v will you get? (ie how many answers; positive, negative, or zero?)

Question 12: If you plug v=0 into the velocity equation, what of value for t will you get? (Give an actual numerical answer.)

If you think about it, I think you will see that there is only one answer. As the stone is going up, its speed is always positive. On the way down, its speed is always negative. But right at the top—for just a split instant—the stone stops, as it turns around. Its speed is neither positive nor negative. It is zero. So the answer to this question is, you will get 1. Because at time t=1 second, the stone is still.

Question 13: When v=0 what is h? (Give an actual numerical answer.)

So it's getting more roundabout here. But we're also starting to answer some harder questions. Because in fact, this is exactly how a Physicist would go about figuring out how high something will go when you throw it! He would start with the observation that at the top, the velocity is zero—and he would work backward from there, to find the height. This is a great example of a problem where knowing all the equations in the world won't help you solve the problem, if you don't also think about the Physics of the situation.

Question 14: What's the point of all this?

If you're scoring yourself, give yourself credit for whatever you wrote down. (No credit if you wimped out and didn't write anything.) But here is how I would put it. Mathematical equations represent reality. When we do Physics, we go through a translation process: we translate a physical question into math, we solve the math, and then we translate the math back into a physical answer. This indirect sort of approach turns out to be a very powerful, very rich way of solving all kinds of problems which would be next to impossible otherwise.

But the danger is that we will leave our common sense behind, and trust the math too much! Math can never represent reality fully. And even when it gives the right answer, if you don't understand the Physics behind the problem, you haven't really learned anything useful or interesting. It's when you are using the math as a tool to give answers to problems that you fully understand—and you fully understand what the math is really doing for you—that it becomes useful, and fun. And the key to that fun is never abandoning your common sense.

That way, when you reach Relativity and Quantum Mechanics, and your common sense is suddenly wrong about everything, the real fun begins!

Epilogue or Appendix or Whatever: The Equations

So: throughout our period of concern, the rock is under the force of gravity, which happens to exert a constant acceleration. That isn't obvious, it's just a law of Physics. But that's where we start.

The equation for motion under constant acceleration is x=x_o+v_ot+½at² where x is the position at any given time, x_o is the initial position, v_o is the initial velocity, and a is the acceleration. This equation is also not obvious; although with a really good understanding of velocity and acceleration, you can derive it slowly using algebra, or very quickly using calculus.

In our case, the position x was actually a height h. The initial position x_o was zero: that is, we started at height zero. The initial velocity v_o was 32: we started at 32 feet per second. And the acceleration was -32, since the acceleration due to gravity happens to be -32 feet/second/second. (Also not obvious: this is just an experimental result.) So the actual height equation we were working with comes from plugging in all these numbers:

h = 32t - 16t2


The general velocity equation under constant acceleration turns out to be v=v_o+at, so our velocity equation is:

v = 32 - 32t


Using those two equations, you should be able to get all the answers. Most of the questions require only very basic algebra: questions 5-9 involve quadratic equations.

As an example, let's take problem 1. We started by saying that t=0. So by the above equation, we see that h=32(0)-16(0)² which is 0. So sure enough, the math gives us what we thought it would.

Note that the "no-answer" problem, number 8, winds up mathematically resolving to the square root of a negative number. This is one of my favorite examples of math, almost magically, doing what it has to in order to give you the right answer. Similarly, you will get one valid answer for question 5, and two valid answers for question 6. Try it!

Send comments or questions to the author