Copyright (c) 1996 by Kenny Felder
How to Read This Paper Skimming lightly over this paper to get the main ideas will do you about as much good as skimming the Rosetta Stone. If you want to get anything out of this, you really need to set aside a few hours to really read every paragraph, think about (and question) every concept, and work every problem before you read the answer. I can't emphasize this too much: make sure you really understand every paragraph before you go on to the next. These may well be the most difficult (and wonderful) concepts that you have ever seen in your life, and they aren't going to come easily.
Math I'm not going to assume any mathematical knowledge here, other than the ability to subtract 2 thousand from 5 thousand (or 1/4 from 1). I am going to assume that you don't melt into slag when you see numbers. If you got through the sentence-before-last as solid matter, you should be all right.
Structure I'm going to start out by explaining Galilean Relativity; this concept, more than any other, must be understood before you can appreciate the modern stuff at all. So fasten your seatbelts and hop on board the Way-Back Machine, as we head for the seventeenth century …
Galilean Relativity is a part of what we now call "Classical" or "Newtonian" Physics. Newton's Physics is a very good system for predicting the motion of everything from falling apples to rotating planets, which is why it held sway for so many hundreds of years. It's also very intuitive; which is to say, once you think about it, it kind of makes sense. So when you're reading this part, make sure that it seems to be talking about the same universe you're living in. That way, when you lose that intuitive grasp in the twentieth century, you'll miss it.
Also, as I mentioned earlier, be sure to work the problems before you read the answers. You won't need a pen and paper, but you will need to think.
Question #1: I'm driving in a car going thirty miles an hour. You're standing by the side of the road watching me go by. After I pass you, you throw a frisbee at me at thirty miles an hour. How long does it take for the frisbee to catch up with me?
Answer #1: Score yourself ten intuition points if you said it never catches up. Never mind that the frisbee is hurtling towards me at thirty miles an hour: I'm travelling away from it at the same speed, so it doesn't ever catch me. Makes sense so far, right?
Now, let's put a two-year-old in the car with me. Being an egocentric little tyke, he tends to assume that he's never moving. When he looks out the window and sees trees zipping past, he just figures that the trees are racing by. He certainly doesn't conclude that the car, with him in it, is moving past the trees.
So what does the two-year-old think the frisbee is doing? (To ask the same question in Physics jargon, what's the frisbee doing in the two-year-old's "reference frame"?) The frisbee is just hanging in space behind the car, not moving at all. So if we ask the two-year-old the question I asked you (when does the frisbee catch the car?) he gets the same answer you did (it never catches up), but for a completely different reason. You and I have common sense, which tells us that the car is really what's moving and the trees are really standing still, but it is interesting to notice that the two-year-old in the car gets the same answer we did: the frisbee never reaches the car.
Now comes brain strain time. The two-year-old is as correct as we are. If he wants to say that the car isn't moving but the trees are, he's right; if you want to say that the trees aren't moving but the car is, you're right too. Because for any question you ask (such as the one I discussed above about the frisbee catching up), he will get the same answer you do. Scientifically, if he gets all the right answers, there's no basis for saying that his assumptions are wrong; even if his assumptions violate common sense as absurdly as the notion that the car is standing still and the trees are rushing backward.
Going one step further, you can pick anything you want - the sidewalk, the car, or an SST going overhead - as "stationary," assume everything else is moving, and you'll be perfectly successful in predicting the universe. This result is summarized in the following statement: the laws of Physics work in any inertial reference frame. Which is just a fancy way of saying that the two-year old is perfectly correct in believing that he's not moving, as long as he's consistent about everything.
(This phrase "inertial" is pretty critical here: it means that you only count as a reference frame if you are not accelerating, which is to say, if you are not speeding up or slowing down or changing direction. If the driver suddenly slams on the brakes, our little two-year-old will darn well know that he's not standing still, as he feels his body slamming against the seat belt!)
If you think this is just mathematical double-talk, consider this: the trees really are moving. They're spinning around the Earth's center, and around the sun, faster than the fastest airplane you've ever been in. If you say that the people in the car "really are" moving, and they should have to know that they're moving before they try to describe reality, then you have to say that no one will do any real Physics until we can float at some God-fixed point in space, and everything we've figured out so far is just lucky.
Well, all that's not so unintuitive, is it? I mean, it may be a slightly odd way to look at things, but after a while it starts to settle comfortably in your mind. That's the wonderful thing about classical Physics. Let's try a couple of probing questions to test the concept.
Question #2: I'm moving away from you at thirty miles an hour (as in the last question), and you throw a forty mile an hour frisbee at me. So this time, the frisbee catches up; and when it does, it hits me in the head. Now, I've been hit in the head by a lot of frisbees, and I can always tell how fast they're going by how much it hurts. How fast was this frisbee going, by that test? (In fancier words, the frisbee is going forty miles an hour in your reference frame; how fast is it in my reference frame?)
Answer #2: The answer is: in my reference frame, the frisbee is travelling ten miles an hour. To follow up the pain metaphor, the bump on my head is exactly the same size as my last ten-mile-an-hour bump, and nowhere near my forty- mile an hour bump a few months ago.
As in the last problem—as in any relativity problem—we have the measurable facts (which we must agree on) and the explanation (which we might totally disagree on). The measurable fact is that the frisbee inflicted a ten-mile-an-hour bump. Incidentally, if this bump analogy is giving you a headache, just say I have a perfect speed-measuring machine with me. The point isn't the device, the point is the result it measures.
Anyway, we now get to the part we disagree on, the explanation of the ten-mile-an-hour measurement. From your reference frame, it was a darn fast frisbee, but the impact was softened by the fact that I was moving away in my car. From my frame, I was standing still (I'm always standing still in my own frame), but the frisbee was only coming on at ten miles an hour. Either way, we agree that it doesn't hit me too hard. And, as I mentioned before, the important thing is that we agree.
Everything I've said so far is old news in the Physics community, which may lead you to wonder why I'm going through all this pre-Einstein stuff in a paper about Special Relativity. Well, first of all, I want to introduce the classical concept of a reference frame: that concept, and the rule that the laws of Physics are the same in all reference frames, is central to Einstein's work. And second, I want you to understand the proof in the next paragraph. I will get to Einstein soon, but when I do, I will refer to this proof a lot, so you have to understand it.
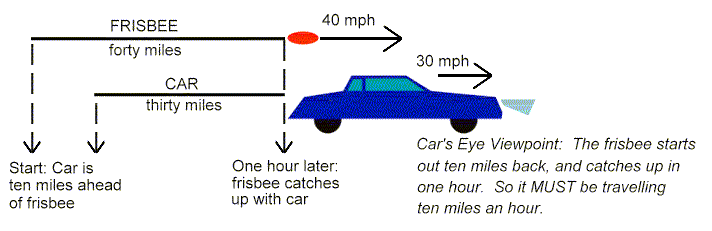
So: a proof that, in my (travelling) reference frame, the forty-mile-an-hour frisbee really is going ten miles an hour. To start with, let's assume that you throw the frisbee after I pass you, and it takes an hour to catch me. How far did the frisbee travel in that hour (in your non-moving reference frame)? The answer is forty miles: by definition, that's what it means to say "the frisbee is travelling at forty miles an hour." If you got that, the next question should be a snap: how far did I travel in that hour? Thirty miles, because I'm driving at thirty miles an hour. So what do I see? The frisbee starts out ten miles behind me, and, in the course of an hour, it catches up. So, by definition, I must see the frisbee travelling ten miles an hour. Because every hour, it gains on me by exactly ten miles.
This is the crucial explanation, and I want you to note one thing about it in particular. It makes no reference to bumps on the head or any other speed-measuring tools. The tools are not the point: the velocity change occurs as a result of the definitions of distance and speed, and all the tools do is measure that change. The change is real. At this point reread the last paragraph, and look at the following diagram, until you are absolutely convinced that "ten miles an hour" is the only possible answer to Question #2. We're coming up on the most important moment in this paper, and it won't be any fun at all unless you are completely with me so far.

Question #3: (Same question, bigger numbers.) If light from a nearby star travels at 200 thousand miles per second, and you're in a spaceship moving away from that star at 50 thousand miles per second, how fast in your frame is the light moving?
Answer #3: I hope you got 150 thousand miles per second. The principle is the same as with the frisbee and the car, it's just a little faster. 200 thousand minus 50 thousand must give the answer. All makes sense so far, right?
Well, one of the games in the late nineteenth century was measuring things like this. A couple of Physicists named Michelson and Morley (among many others) came up with a very clever experiment designed to measure the speed of the light both parallel to, and perpendicular to, the Earth's motion. And what they got, unfortunately, seemed to disagree with my Answer #3 above. In fact, what Michelson and Morley seemed to find was that the speed of light was exactly the same no matter how they measured it, whether it was moving with, against, or perpendicular to the motion of the Earth. Let me repeat that. Experiments show that no matter how fast you're moving, and no matter what direction you're moving in, you get exactly the same answer when you measure the speed of light. Dramatic music.
If you aren't very surprised right now—if it doesn't bother you that the answer "150 thousand miles per second" is wrong—then please do me a favor. First, convince yourself that this is exactly the same problem as Question #2, except that the numbers are bigger. Second, go back to Answer #2 (especially to the "proof" paragraph), and try to find a flaw in the argument. Do this before you go any further.
On the other hand: if you're starting to get irritated and wonder when I'm going to admit that 150 thousand mi/sec really is the answer, then I congratulate you on not believing everything you read. You're in good company: the late-nineteenth-century scientific establishment, which included some of the greatest minds in history, was completely incapable of believing this result. Michelson himself went to his grave not believing that Galilean Relativity could be dismissed. So my advice to you is, fight with this concept for a moment. Try to disprove it. Treat it as a science fiction excercise: if we lived in a universe where Galilean Relativity didn't work, what else would be different? What contradictions can you find?
Galileo, as I mentioned earlier, lived in the seventeenth century. By talking about light instead of frisbees, we have leapt headlong into the twentieth century, when Albert Einstein asked the same questions you're probably asking yourself. In 1905, he published his answers in his first paper on The Special Theory of Relativity. You've probably been wondering when that phrase would surface in this paper. Well, here it is.
Einstein's theory can be stated briefly as: the speed of light is the same in all inertial reference frames. You on the sidewalk, me in my car, and an astronaut going by in a super-rocket will all get very different answers if we measure the speed of a frisbee; but we will all get exactly the same answer when we measure the speed of a beam of light. The answer we get is roughly 186,000 miles per second, which is a messy number: so I'll keep using 200,000, or else I'll just do what scientists do, which is forget all about the number and use the letter c to mean the speed of light. Scientists always prefer letters to numbers anyway.
Note, incidentally, that you couldn't possibly choose the letter f to stand for the speed of frisbee, because that speed depends on who threw the frisbee, how hard he threw it, and what reference frame it's being measured in. The speed of light, however, doesn't depend on any of that, which is why we can give it a letter.
So Einstein postulated that c is constant. That statement formed the basis for his Special Theory of Relativity, and it certainly solved the problem of explaining why Michelson and Morley didn't see what they expected. It's not an entirely intuitive result, but it patches the gap without rocking the rest of Physics, right?
Perhaps you're starting to get a bit suspicious when I end a paragraph with the question "right?". Well might you be. The problem in this case is that Newtonian Physics is a pretty tightly woven web, and if you pull one string out the whole thing unravels pretty quickly. To demonstrate that, it is only necessary to take Einstein's postulate and play with it a bit. Let's go back to the picture above. I'm back in my car, only now it's travelling at 1/4 c (one-fourth the speed of light). You shine a flashlight at me, and we both measure the speed of the light ray. Obviously, you measure exactly c. Intuitively, we might say that I measure 3/4 c; but we now have Einstein telling us that no, I also get exactly c. So far, so good.
The problem comes when you remember my proof, earlier, of the intuitive result. If you see the flashlight beam travelling at 200 thousand miles per second, that means that every second, the beam front is 200 thousand miles further ahead of you. If I see the flashlight beam travelling at 200 thousand miles per second, that means that every second, the beam front is 200 thousand miles further ahead of me. This has nothing to do with how we measure things, it just comes from the definition of velocity.
Now we are at the heart of the paradox. After one second, you're still where you were - I'm 50 thousand miles ahead of you - and we both see a beam of light 200 thousand miles ahead. Take a minute and see if you can find a way out of the dilemma. After a minute of thinking about this point, I think you will sympathize a lot more with the people who refused to accept relativity.
What we have here is a rock-solid proof that the speed of light must change; and a lot of experiments that show that the speed of light does not change. Whenever a good proof goes bad, you have to start questioning the premises that you built your proof on. What did I assume when I demonstrated that the speed of light had to change? Well, not much; but I certainly assumed that you and I would both had incredibly good clocks when we measured things like "one second" or "one hour." What if our clocks disagreed? I would say "it was 200,000 miles ahead of me after one second." You would reply "No, your clock's wrong; you made that measurement after a second-and-a-half. After one second, it was actually 200,000 miles in front of me." And so we would disagree, but there wouldn't be any paradox.
This is how Einstein disproved the proof and resolved the contradiction. He said that our clocks will disagree, even if we both have the best clocks in the world. This is not a feature of clocks: it is a feature of time itself. (I'm going to talk a lot about clocks in the rest of this paper. Assume that all the clocks work perfectly, and remember: what we say about a perfect clock, we are actually saying about time. The clock is just a way of measuring the flow of time. As always, it's the thing measured—not the measuring device—that matters.) So when Einstein says that our clocks will disagree, he's actually saying that time will be different for you and me. The rest of this paper will be entirely devoted to that single mind-boggling concept, but first let me summarize what we've got so far.
We started with experiments that showed that, despite our intuitive idea that speeds should depend on the speed of the observer, the speed of light is always the same. That fact, which came from experiments, had to be integrated into theory—so Einstein postulated that the speed of light, unlike the speed of other things, does not change in different reference frames. From that, it was a short step to prove the following result: observers in different reference frames experience time differently. Now, that's some pretty heavily unintuitive stuff, sounding more like the Planet of the Apes than the Breakthrough of the Physicists—but there it is. The Special Theory of Relativity, Short Form: "The speed of light is constant by experiment, therefore all kinds of unintuitive things by logic." Most of the game of relativity is exploring those unintuitive things, and the paradoxes they lead to, in order to increase our feel for the universe Einstein claims we live in.
Question #4: You're standing on Earth as I go by in my rocket. When you look at my clock, you notice that it's running slowly because time runs slowly in my reference frame. When I look at your clock, what do I see? Is your clock running slow, fast, or right on time?
Answer #4: Score yourself a "good try" point if you said that I see your clock running fast. But don't get too excited, because the actual answer is: I see your clock running slow. Just like you see my clock running slow.
That's right, it was something of a trick question. It's the most natural thing in the world to think that if you see my clock running slow, I should see your clock running fast. But then you have to ask the question: when I flew by, who decided that you should be fast and I should be slow? Why not the other way around? After all, my frame (in which I'm not moving but you are) is just as valid as your frame (in which the Earth isn't moving but the rocket is). So, by symmetry, we must see the same thing! If you see my clock running slow, I have to see your clock running slow!
Which proves I'm right; but it doesn't get us out of the paradox. It still doesn't make sense for us both to see each other's clocks moving slowly: if you're still with me, this should seriously bother you. (If you're not still with me, take a break and come back. Long paper, complicated subject.) When you have a paradox that won't go away easily, you design a thought experiment to look at that paradox as closely as possible. Then either the paradox goes away, or you have a good disproof of the theory. So let's look more closely at this both-of-us-see-each-other's-clocks-going-slow business.
Thought Experiment #1: You're on Earth, and I fly by in my rocket as before. Right as we pass each other, we both start our stopwatches. When your stopwatch says that one minute has passed, you check my stopwatch. Because I'm in a different frame, my watch is running slow: it only says thirty seconds.
Now let's play that exact situation back from my frame. You looked at me after only thirty seconds; but your clock was running slow, so it said only fifteen seconds. CONTRADICTION! We agree that when you looked at me, my watch said thirty seconds: but did your watch say fifteen seconds (as I thought), or sixty (as you thought)? So we have taken what we intuitively felt made no sense, and exploited that to come up with a paradox that will test relativity: if there isn't a way out of that paradox, Relativity falls.
So, as you probably suspected, here is the way out of the paradox. The problem, as with most of modern Physics, comes in making the measurement. Suppose that when I passed you the first time, and we synchronized our watches, we were right next to each other. That means that sixty seconds later (your frame), when you checked my watch, I was a long way away. How do you look at my watch a long way away? Your eyes take in light that bounced off it; your ears take in sound coming from it; whatever you do, you're using something that travelled from me to you. And it took time to do it.
The point is, you can't say "I'm looking at his watch now." You have to say "I'm looking at light that came from his watch a while ago," and I have to say the same thing when I look at you. So when you and I are in different places, whatever we see about each other is old news. And we have to take that into account when we say "This is what I'm seeing on his watch," admitting that this is simply what his watch used to say. When we take that into account, we can plug through the math of Einstein's equations and we wind up without a paradox.
Well, that was a sneaky way out. Looks like we can't disprove Relativity unless we can make measurements from the same place, at the same time, twice! Which we clearly can't do if one of us is moving, right?
Well …
Thought Experiment #2: The Paradox of the Twin. When paradoxes have their own names, they tend to be pretty simple. So it is with this one; the Paradox of the Twin is actually simpler than the experiment I discussed above, although you will see how it comes in response to that one.
Two twin brothers, Astro and Clay, bid a tearful farewell as Astro journeys into space. Astro is gone for twenty earth years, but because he is moving so incredibly fast, his clock is running very slowly and only a year passes in his own frame. When he returns, Clay is gray-haired and wrinkly, while Astro is still young and healthy. Based on Relativity, it makes perfect sense to say that less time passed for Astro because his clock was running slow. But then you can ask, what happened from Astro's perspective? He wasn't moving, and Earth was; so Clay's clock was moving slowly; so shouldn't Clay be the young one? CONTRADICTION. Think about that for a while. Does Einstein have a way to wriggle out of this one?
As before, yes, he does; and yes, it's sneaky and weird. Astro doesn't have an inertial reference frame. You can't look at things from his perspective, because he turned around in mid-flight. I mentioned earlier that an "inertial reference frame" means one which keeps on travelling at a constant speed. When Astro turned around; when he lost his stomach because the rocket was suddenly stopping and starting up again in the other direction; he should have realized that he was now in a different reference frame from the one he started in. So all bets are off, as far as Special Relativity is concerned. Clay's perspective tells the true story, and for Astro to calculate his brother's age, he has to take his reference-frame-change into account in his calculations. When he does, he will get the same result Clay got: young Astro, old Clay.
The rest of relativity is a lot like those last two thought experiments, usually done with enough math to rigorously prove the results that I "hand-waved" my way through. You can come up with—and explain—more and more time-dilation paradoxes. Some of your explanations lead to other bizarre relatavistic phenomena. You can show that length is different in different reference frames, destroying the classical concept of space; that mass is different in different reference frames, destroying the classical concept of matter; and that mass and energy are the same thing, destroying the classical concept of a winnable war. And Einstein did all of this, in the first decade of this century. His theory explained what happens when things go astonishingly fast, just as Quantum Mechanics was explaining what happens when things get amazingly small. (And Einstein went on to form the General Theory of Relativity, which explains what happens when things get incredibly big.) All of this is the wonder of modern Physics, the lure that drew me and so many others into the field: concepts which are as far out as any of science fiction or fantasy, are real, and can be analyzed and discussed intelligently rather than kind of mumbled about. And now that you have made it all the way through this paper, you can talk more intelligently about them than most. And maybe—hopefully—you're starting to wonder what else you can say about them.
Einstein Light has cool video clips with demonstrations and animation on relativity, and papers that go deeper for the Truly Interested.
 Gary and Kenny Felder's Math and Physics Help Home Page
Gary and Kenny Felder's Math and Physics Help Home Page
www.felderbooks.com/papers
 Send comments or questions to the author
Send comments or questions to the author