Tutorial 1: Lines in Curved Space

Before we talks about the characteristics of shapes in curved space, it is important that we cover the basics. In order to define the concept of a triangle, we will first need to think about the idea of a line in curved space. What is a line is curved space? How is it defined?

Lines on a Sphere

In curved space, the concept analogous to a line in flat space is called a geodesic. The definition of a geodesic can be thought of in two different equivalent ways. First, a geodesic is the path that is locally as straight as possible. Imagine you are at the North Pole of the Earth, and you take 100 steps South along the Prime Meridian. It appears that you have followed a straight path; in fact, you have walked the straightest possible path between your starting and ending points. However, if you continued to follow the Prime Meridian (and subsequently the 180-degree longitude line) you would eventually arrive back at the North Pole. While this is not what we traditionally think of as a line in flat space, it is a geodesic in curved space, because locally, the path we followed was as near to straight as possible.

Geodesics can also be thought of locally as the shortest path between two points. In the previous example, you walked straight for 100 steps along the Prime Meridian; you also followed the shortest path between your starting and ending points. If you continued to walk the shortest segments along the Prime Meridian, you would follow the same geodesic you followed for the first explanation. The two explanations are equivalent; you can either think of locally following the straightest path or the shortest path.

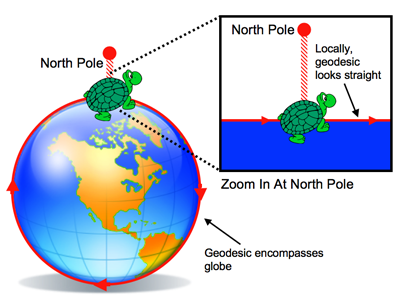
In 2-dimensional space of constant positive curvature we sometimes also refer to geodesics as great circles, or circles that encompass the sphere at its largest point. If you follow locally straight paths until you reach the point where you started, you will always follow great circles around the sphere. (Check to see that this is true.) On a globe, longitude lines are great circles, or geodesics, because they encircle the globe at its largest point. However, latitude lines are generally not great circles; if you look at a map of the Earth you might guess that the fastest way from Anchorage to Stockholm is to fly West along the 60-degree-North latitude line, but the fastest way is actually to fly over the top of the globe, near the North Pole. You can map great circles (or geodesics) connecting cities on the globe using this website, created by Karl Swartz.

When you take steps in CurvedLand, you follow geodesics. You can see this; any step you take looks locally like the shortest and straightest path between your starting and ending points. When you draw true lines in CurvedLand, the shapes drawn are geodesics, or lines following great circles on the surface of a spherical embedding diagram. However, you can see how these geodesics differ from lines in flat space; if you follow a locally straight path in one direction for long enough, you will eventually end up back where you started. Also, if you draw a true line (geodesic) or if you turn the trail on and follow a straight path and then move away from that path, the created lines, or geodesics, do not always look straight. When you view geodesics from some outside position, they will not always look like the shortest path between two points. Additionally, when you zoom in, all of the geodesics appear to be straight, but as you start to zoom out, some appear curved. This is because, locally, geodesics appear straight, but when viewed from afar, they appear to curve.

Copyright (C) 2010 Stephanie Erickson, Gary Felder
Terms and Conditions of Use