

Next: Occupation Number and Energy
Up: Definitions of Number and
Previous: Rescaled Fourier Transforms
The equation of motion for a scalar field in an expanding universe
is
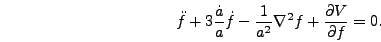 |
(5.10) |
To define an adiabatic invariant occupation number for this field
we need to switch to conformal variables in which this equation
becomes a more standard oscillator equation. These variables are
 |
(5.11) |
Using conformal time and noting that
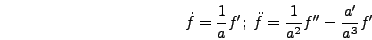 |
(5.12) |
the equation of motion becomes
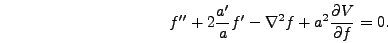 |
(5.13) |
Then switching to conformal field values note that
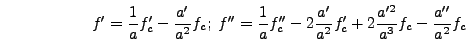 |
(5.14) |
and thus
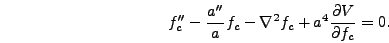 |
(5.15) |
This equation can be approximated in Fourier space by
 |
(5.16) |
where
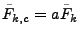 and
and
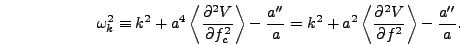 |
(5.17) |


Next: Occupation Number and Energy
Up: Definitions of Number and
Previous: Rescaled Fourier Transforms
Go to The
LATTICEEASY Home Page
Go to Gary Felder's Home
Page
Send email to Gary Felder at gfelder@email.smith.edu
Send
email to Igor Tkachev at Igor.Tkachev@cern.ch
This
documentation was generated on 2008-01-21