

Next: Program Variables
Up: Definitions of Number and
Previous: Conformal Coordinates
In terms of the conformal variables of the previous section it
makes sense to define occupation number as
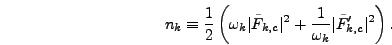 |
(5.18) |
Note that this quantity is adiabatically invariant, meaning it is
conserved in the limit
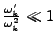 . Note
also that because it is defined in terms of
. Note
also that because it is defined in terms of 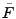 instead of
instead of
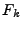 ,
, 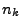 is unitless.
is unitless.
The energy density 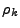 is defined as
is defined as
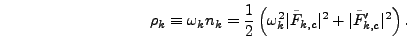 |
(5.19) |
To convert these definitions back to physical coordinates note
that
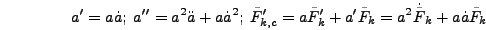 |
(5.20) |
so
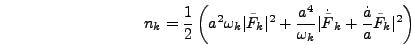 |
(5.21) |
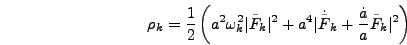 |
(5.22) |
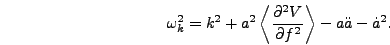 |
(5.23) |
Finally, in terms of the discrete Fourier transform 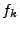
![\begin{displaymath}
n_k = {a^2 dx^6 \over 2 L^3} \left[\omega_k \vert f_k\vert^2...
...omega_k} \vert\dot{f}_k + {\dot{a} \over a}
f_k\vert^2\right].
\end{displaymath}](img167.png) |
(5.24) |
![\begin{displaymath}
\rho_k = {a^2 dx^6 \over 2 L^3} \left[\omega_k^2 \vert f_k\vert^2
+ a^2 \vert\dot{f}_k + {\dot{a} \over a} f_k\vert^2\right].
\end{displaymath}](img168.png) |
(5.25) |


Next: Program Variables
Up: Definitions of Number and
Previous: Conformal Coordinates
Go to The
LATTICEEASY Home Page
Go to Gary Felder's Home
Page
Send email to Gary Felder at gfelder@email.smith.edu
Send
email to Igor Tkachev at Igor.Tkachev@cern.ch
This
documentation was generated on 2008-01-21
![]() is defined as
is defined as