

Next: Energy Density
Up: Definitions of Number and
Previous: Program Variables
Number and Energy Spectra in One and Two Dimensions
The ordinary power spectra
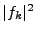 and
and
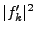 are output in the same way regardless of the number of dimensions, but the spectra
are output in the same way regardless of the number of dimensions, but the spectra 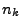 and
and 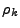 have well defined normalizations, so in one and two dimensions they are normalized so as to try to approximate the values that they would have in three dimensions. Let
have well defined normalizations, so in one and two dimensions they are normalized so as to try to approximate the values that they would have in three dimensions. Let 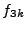 be the Fourier transform of a three dimensional field
be the Fourier transform of a three dimensional field 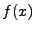 , and let
, and let 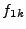 and
and 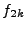 be the Fourier transforms of the field taken on one and two dimensional slices respectively. Assuming that isotropy holds on average we show in section 6.3.5 that
be the Fourier transforms of the field taken on one and two dimensional slices respectively. Assuming that isotropy holds on average we show in section 6.3.5 that
 |
(5.36) |
and
 |
(5.37) |
Recall that the wave vector 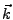 is given by
is given by
 |
(5.38) |
where 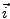 is the position on the grid in Fourier space (i.e. a triplet of integers from
is the position on the grid in Fourier space (i.e. a triplet of integers from 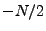 to
to 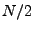 ). Thus
). Thus
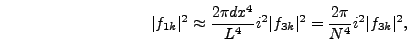 |
(5.39) |
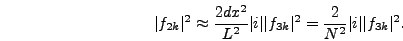 |
(5.40) |
The Fourier transform 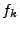 that is actually calculated in one and two dimensional simulations will correspond to
that is actually calculated in one and two dimensional simulations will correspond to 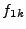 and
and 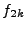 . The definitions of
. The definitions of 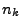 and
and 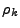 , however, are given in terms of
, however, are given in terms of 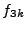 . Thus equations [5.33] and [5.34] are multiplied by prefactors equal to
. Thus equations [5.33] and [5.34] are multiplied by prefactors equal to
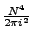 and
and
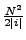 in one and two dimensions respectively.
in one and two dimensions respectively.


Next: Energy Density
Up: Definitions of Number and
Previous: Program Variables
Go to The
LATTICEEASY Home Page
Go to Gary Felder's Home
Page
Send email to Gary Felder at gfelder@email.smith.edu
Send
email to Igor Tkachev at Igor.Tkachev@cern.ch
This
documentation was generated on 2008-01-21
![]() and
and
![]() are output in the same way regardless of the number of dimensions, but the spectra
are output in the same way regardless of the number of dimensions, but the spectra ![]() and
and ![]() have well defined normalizations, so in one and two dimensions they are normalized so as to try to approximate the values that they would have in three dimensions. Let
have well defined normalizations, so in one and two dimensions they are normalized so as to try to approximate the values that they would have in three dimensions. Let ![]() be the Fourier transform of a three dimensional field
be the Fourier transform of a three dimensional field ![]() , and let
, and let ![]() and
and ![]() be the Fourier transforms of the field taken on one and two dimensional slices respectively. Assuming that isotropy holds on average we show in section 6.3.5 that
be the Fourier transforms of the field taken on one and two dimensional slices respectively. Assuming that isotropy holds on average we show in section 6.3.5 that
![]() that is actually calculated in one and two dimensional simulations will correspond to
that is actually calculated in one and two dimensional simulations will correspond to ![]() and
and ![]() . The definitions of
. The definitions of ![]() and
and ![]() , however, are given in terms of
, however, are given in terms of ![]() . Thus equations [5.33] and [5.34] are multiplied by prefactors equal to
. Thus equations [5.33] and [5.34] are multiplied by prefactors equal to
![]() and
and
![]() in one and two dimensions respectively.
in one and two dimensions respectively.