
Next: The Adiabatic Approximation
Up: Initial Conditions on the
Previous: Initial Conditions in One
The Initial value of the Hubble Constant
The initial value of the Hubble constant is used for setting the field
derivatives (equation (6.72)) and as an initial condition
for the second order evolution equation for the scale factor. The
derivative of 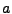 is determined by the equation
is determined by the equation
 |
(6.87) |
Initially 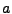 is set to
is set to 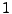 and
and
 |
(6.88) |
In setting initial values we assume all inhomogeneities are small and
thus use only the homogeneous values of the fields 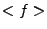 and
and
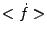 . Typically the initial field values will be one for the
inflaton and zero for all other fields but they can be set to any
values by the user. In general, the initial energy density is thus
. Typically the initial field values will be one for the
inflaton and zero for all other fields but they can be set to any
values by the user. In general, the initial energy density is thus
 |
(6.89) |
Converting to program variables
where the second step uses the fact that initially 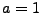 . Since
initially
. Since
initially 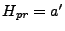 we can plug equation (6.90) into
equation (6.88) to get an equation we can solve for
we can plug equation (6.90) into
equation (6.88) to get an equation we can solve for
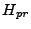 . Solving this quadratic equation gives
. Solving this quadratic equation gives
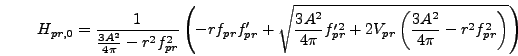 |
(6.91) |
where 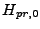 refers to the initial value of
refers to the initial value of 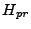 and each term
with field or field derivative values is understood to be summed over
all fields.
and each term
with field or field derivative values is understood to be summed over
all fields.


Next: The Adiabatic Approximation
Up: Initial Conditions on the
Previous: Initial Conditions in One
Go to The
LATTICEEASY Home Page
Go to Gary Felder's Home
Page
Send email to Gary Felder at gfelder@email.smith.edu
Send
email to Igor Tkachev at Igor.Tkachev@cern.ch
This
documentation was generated on 2008-01-21
![]() is determined by the equation
is determined by the equation
![]() and
and
![]() . Typically the initial field values will be one for the
inflaton and zero for all other fields but they can be set to any
values by the user. In general, the initial energy density is thus
. Typically the initial field values will be one for the
inflaton and zero for all other fields but they can be set to any
values by the user. In general, the initial energy density is thus