Requires Fonts

Spooky Action at a Distance

An Explanation of Bell's Theorem

Copyright (c) 1999 by Gary Felder

I. Introduction

There are many aspects of modern physics which seem to violate our intuition. The classical theory of physics which was held from the time of Newton until this century provided an orderly model of a world made of objects moving around and pushing each other around in predictable ways. The mathematics could be difficult, but the basic ideas meshed with our common sense notions of how the world works. Starting at the beginning of this century, our physical theories began to include aspects which ran counter to that common sense, and yet the theories consistently made accurate predictions of experiments which could not be explained with Newtonian physics. Gradually, and despite much resistance, physicists have been forced to accept these new results.

In this paper I am going to discuss one of those results, called nonlocality. Its converse, locality, is the principle that an event which happens at one place can't instantaneously affect an event someplace else. For example: if a distant star were to suddenly blow up tomorrow, the principle of locality says that there is no way we could know about this event or be affected by it until something, e.g. a light beam, had time to travel from that star to Earth. Aside from being intuitive, locality seems to be necessary for relativity theory, which predicts that no signal can propagate faster than the speed of light.

In 1935, several years after quantum mechanics had been developed, Einstein, Podolsky, and Rosen published a paper which showed that under certain circumstances quantum mechanics predicted a breakdown of locality. Specifically they showed that according to the theory I could put a particle in a measuring device at one location and, simply by doing that, instantly influence another particle arbitrarily far away. They refused to believe that this effect, which Einstein later called "spooky action at a distance," could really happen, and thus viewed it as evidence that quantum mechanics was incomplete.

Almost thirty years later J.S. Bell proved that the results predicted by quantum mechanics could not be explained by any theory which preserved locality. In other words, if you set up an experiment like that described by Einstein, Podolsky, and Rosen, and you get the results predicted by quantum mechanics, then there is no way that locality could be true. Years later the experiments were done, and the predictions of quantum mechanics proved to be accurate. In short, locality is dead.

In this paper I am going to describe the proof of Bell's theorem. The mathematics is very simple; I won't ask you to do anything more complicated than count and add.1 The way we will prove the theorem is to assume locality to be true, which will eventually lead us to make a testable prediction. When it turns out that the experiments don't obey that prediction we will be forced to conclude that our assumption of locality was false. As we go, try not only to follow the proof as I present it but also to see if you can find any other assumptions that crept in. If there are any, then perhaps one of those is false and locality is still true. So far, nobody has found any holes in Bell's theorem, but there is no way to understand the proof without trying.

In the next section, The Experiment, I will describe an experimental setup, specifying how our measuring devices will be set up and what kinds of results they can give us. Having described the setup of the experiment, the next two sections, Preliminary Results and The Proof, present some experimental results and attempt to interpret them, culminating in the final proof of Bell's theorem. Finally in Conclusions I will present some final thoughts on our current understanding of physical theories.

There are three appendices which supplement the main body of the paper but are not necessary for understanding the proof. The first, Bell's Theorem and Relativity, will be a discussion of why this result isn't incompatible with relativity's prediction that nothing can travel faster than light. Although this section is not necessary for understanding the rest of the paper, it addresses one of the most common concerns raised about nonlocality. The second appendix, What's Being Measured, fills in some of the gaps left in the very general description of the experiment given in the main body. The final appendix, The Calculation, shows how to use quantum mechanics to predict the exact numerical results of the experiment and discusses in a little more depth the connections between these results and the predictions of relativity.

The particular experimental setup described here was first devised by N.D. Mermin to illustrate Bell's inequality.2

II. The Experiment

The way many physics experiments are done is that you send a particle into a detector and the detector gives some output indicating the result of some measurement it performs on the particle. For example, if the detector is measuring mass and you send in an electron it would give a reading that says something like "10 to the minus 30 kilograms." In our case, we are going to consider the simplest possible output, namely a binary signal. In other words every time a particle enters our detector a light will flash green or red, depending on whether the particle does or doesn't have some specific property we are interested in. So if I send a beam of electrons in, then every time one entered the detector I would see a flash, which would sometimes be red and sometimes green.

At this point you may be wondering what this detector is measuring. Rather than answering that directly, we are going to approach the problem experimentally. We know we have a detector and that it gives some result every time an electron goes into it, and by doing various experiments with it we are going to try to figure out as much as we can about this property it is measuring. This way we can try to ensure that our proof wasn't based on some incorrect assumption about the particular property we are measuring. So everything we conclude about this property should be a result of our experiments, rather than a prior assumption.

Just to give it a name which shouldn't in any way prejudice us as to what is actually being measured I will refer to this property as the electron's "happiness". For example I might try sending the same electron into two of these detectors (assumed to be identical) one right after another. If I find that the two detectors always give the same result when they measure the same electron, then I can conclude that the electron's happiness is stable over time; in other words it doesn't change as it moves between the two detectors.

I should make it clear at this point that although I am deliberately not making assumptions about what these detectors are measuring, I am nonetheless describing the results of real experiments. There are detectors which will give exactly the results I describe, and the fact that any experiment can be done which gives these results will be sufficient for us to disprove locality. For those who want to know more about the actual detectors which act this way and what they are measuring, refer to appendix II.

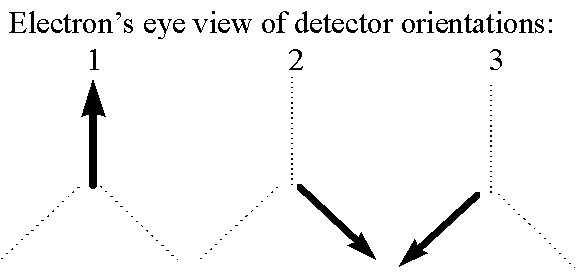
Getting back to our detectors, I am going to make them a little more complicated now. They will still give binary results, but now each detector can be put into one of three orientations: straight up, down/right, or down/left. I call these orientations 1, 2, and 3:

Detector orientations 1, 2, and 3

We presume that each of these three orientations is measuring something different about the electron. So modifying the "happiness" analogy I will say that if an electron enters a detector in orientation 2, the detector measures whether the electron "likes" orientation 2 (in which case the detector flashes green), and likewise for 1 and 3.

Before we go on describing the setup, let's do some experiments with what we've got, and see if we can draw some preliminary conclusions about the nature of the property we're measuring. First of all, we can do the experiment discussed above, where we send an electron into a detector in orientation 1, and then 20 feet later into another detector in orientation 1. As I suggested above, we find that the result is always the same for the two detectors. Some electrons cause both detectors to flash green (they "like" orientation 1) and some cause them both to flash red, but you never see an electron get different colors in the two detectors. So we can conclude that "liking orientation 1", whatever physical property that might really correspond to, is something that stays constant with time. On an even more basic level this result gives us confidence that the detector is in fact measuring something about the electron and not just randomly flashing colors. We can repeat the experiment with both detectors in orientation 2 or both in orientation 3, and the results are the same. All three detector orientations are measuring real quantities which stay constant in time.

One obvious thing to try next is putting up two detectors in different orientations. Say I pass an electron through an orientation 2 detector and then 20 feet later I pass it through an orientation 1 detector. In this case I find that sometimes the two flash the same color and sometimes it is different. Trying this with all possible combinations I can conclude that we are in fact measuring three distinct properties of our electrons. An electron which likes orientation 1 may or may not like orientation 2, and so on. So we can model our electrons with the following picture. Each electron "knows" at any given moment which of the three orientations it does or doesn't like, so we can imagine that the electron is carrying a card with a good or bad mark in each of the three orientations, like so:

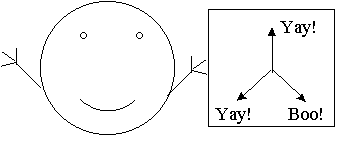
An electron that has properties 1 and 3 but not 2

An electron that has properties 1 and 3 but not 2 (artist's representation)

It may seem like I am belaboring this point, but in order to make our proof solid we want to be very sure that we are not assuming anything. So putting metaphors aside for the moment, we can say that we have concluded so far that our detectors are genuinely measuring some properties of our electrons, that an electron may independently have any combination of the three properties being measured, and that an electron which has some property keeps it, at least as long as it is flying in an undisturbed path between two detectors.

There are many more things we could do at this point, like seeing if there are correlations between these properties or seeing what happens if we string three or more detectors in a row. Rather than pursuing such questions, however, we are going to make our experiment a little more complicated again. Now we are going to set up two detectors on opposite sides of the room, and a source in the middle which shoots out electrons in pairs, each going in opposite directions. In other words a typical experiment will consist of the source firing off two electrons, each one going in a different direction to a different detector, and each one being measured by that detector. The detectors may or may not be pointing the same way. This is the final setup we will need, and by analyzing the results of these experiments we will be able to prove Bell's theorem. Once again it is easiest to talk about things if they have names, so I will call the two detectors A and B. I will use the same names for the electrons, so that the electron going to detector A is electron A and so forth.

This setup with the two detectors is going to allow us to talk about locality. If we assume that the two detectors are far enough apart, and the measurements are done at almost exactly the same time, then locality says that nothing which happens at one of the measurements can affect the result of the other one. We will use that assumption to predict the experimental results, and we will discover that the actual results do not follow our prediction.

III. Preliminary Results

To begin with, let's try pointing both detectors the same way. We find a very simple result: the detectors always flash the same color as each other. If I put both detectors in orientation 2 for example, then maybe the first pair of electrons both flash green, the next pair also both flash green, and the next pair both flash red; but the two detectors are always the same as each other. This result should tell us something about our source. Before reading on, try to state clearly what it is that we can conclude from this first observation.

The conclusion is that the electrons come out of the source with the same properties. In other words if electron A likes orientations 2 and 3 but not 1, then electron B of the same pair feels the same way. Each pair might have different properties, but the electrons within a pair are identical. There is nothing mysterious about this result (and it certainly doesn't violate locality). It's as if someone at a radio station were broadcasting a show and people at two ends of the city were listening to it. They both get the same signal, not because there is any communication between them, but because the source is wired in such a way that it always sends the same signal out in all directions. Likewise, our electron source is set up in such a way that it always sends out pairs of identical electrons.3

This result also seems to bolster what we had already concluded, which is that whatever properties an electron has when it leaves the source can't change in mid-flight. If the properties of one electron changed, but not the other, then they could give different results. You might argue that they could both be changing in some predictable way that keeps them in synch, but you can test (and disprove) this theory by moving one detector a little closer to the source than the other. When you do so the results are unchanged, whereas if the electrons were changing as they flew and you measured one earlier than the other you would expect again that you might get different results. If you still wanted to say they were changing as they flew then you would have to say that the instant one of them was measured the other for some reason stopped changing so that when you measured it later it gave the same result as its partner. Such a scheme would violate our assumption of locality, so we already have an example of how making this assumption constrains what interpretations we can make of our results.

IV. The Proof

Here comes the mathematical analysis, but don't panic. As advertised, you won't need any math more complicated than the ability to add small numbers. I am going to propose another set of experiments we can do with our setup, but before looking at the results we are going to make some predictions about them. After all, that's what science is all about - using your theories to make predictions which you then compare to experimental results.

The experiment I propose is one in which the orientations of the two detectors are set independently and randomly. In other words, each time my source emits two electrons, I throw a die to decide whether to put detector A in orientation 1, 2, or 3. Meanwhile someone at detector B does the exact same thing. The question I want to ask is: "How often will both detectors flash the same color?"

(Don't let the idea of randomness here confuse you. All that matters is that the results of my random choice give me orientations 1, 2, and 3 equal amounts of the time, and that the results at the two detectors are not correlated with each other. Dice, for example, would accomplish both of these quite nicely.)

We know that each electron has a fixed set of properties (represented above as its "card") from the moment it leaves the source. This set of properties can be viewed as a set of instructions for the detector, such as: "Make the detector flash green if it is in orientation 1 or 2 but red if it is in orientation 3." Moreover, we know that both electrons in a given pair have the same set of properties. These sets of properties, or instructions sets, can be broken down into two categories.

Some electrons either like, or dislike, all three orientations. For example, an electron might be "programmed" to cause a detector to flash red no matter how the detector is set. Since the other electron in the pair would of course have the same programming, such a pair guarantees that the two detectors will always give the same result, no matter how you point them. Some electrons, on the other hand, feel one way about one orientation and the other way about the other two. For example, an electron might like orientation 2 (green flash if detector points that way) and dislike orientations 1 and 3. In that case, since the detectors are being set randomly, each detector will give a green flash exactly 1/3 of the time. Given that, let us return to our experimental question: in this case, how often will the two detectors give the same result?

This is the one actual calculation in the proof, and I strongly urge you to try it before reading the next paragraph. To restate the question: You have two electrons, each of which will give one color flash 1/3 of the time and the other color flash 2/3 of the time. Assuming the two results are independent, i.e. both detectors are independently and randomly oriented, how often will both of them give the same result?

To answer that, let's consider the specific example just given (green for 2 and red for 1 or 3). When you point both detectors in randomly chosen positions, there are nine possibilities for how they will end up: A in position 1 and B in position 1, A in position 1 and B in position 2, etc.. These can be laid out in a grid as follows:

Detector A's Position
1 2 3
Detector B's Position
1 S D S
2 D S D
3 S D S

Every configuration for which the two detectors will flash the same color is marked "S", whereas every one for which they will flash different colors is marked "D". For example, if detector A is in position 2 and detector B is in position 3 then they will flash green and red respectively, so this box has a "D" in it. The only way for the two detectors to flash different colors in this example is if one of them is in position 2 and the other one is in position 1 or 3, which corresponds to the four boxes checked "D" in the table.

So what's the probability that they will flash the same color? There are 9 possible configurations for the detectors, and in 5 of them, the two detectors give the same result. Since we assume the detector positions are set randomly each one of those configurations should be equally likely, so the answer is that they will flash the same color 5/9 of the time. In other words, if we run the experiment 9 million times, each of the nine configurations shown will occur about 1 million times, so the two colors will be the same about 5 million times. Of course we don't expect that in 9 million tries we would get the same color at both detectors exactly 5 million times, but as you do more and more trials the fraction of times that the result comes out that way should get closer and closer to this predicted value.

The previous paragraph contained all the math we will need for our proof, and it also led us to the key conclusion of the paper. Once you accept the result we just demonstrated, the rest follows pretty quickly. So please don't skim over the numbers or take my word for it; work it out for yourself and check my work until you are convinced that the number 5/9 is the correct answer to the question the last paragraph was considering.

Now that you are convinced, let me summarize where we are right now.

Now in practice we don't know whether we expect to get the result that the two are the same 5/9 of the time or that the two are always the same, because we don't know enough about our source. If it gives instructions like "always cause a green flash" then we will get perfect agreement, whereas if it gives instructions like "green for 2 and red for 1 or 3" then we will get agreement 5/9 of the time. (Remember that the "instructions" are simply a shorthand way of talking about what values of the three properties a given electron has.) There is no reason to assume, however, that the source always gives the same instructions; it might emit a pair of electrons with the "always red" instructions and then another pair with the "green for 2 or 3 and red for 1" instructions. The important thing is that every time it emits a pair we know that it gives them both the same instructions, so that each time the source emits a pair of electrons the probability of both detectors flashing the same color is either 5/9 or it is 1, i.e. certainty. Thus if we do the experiment many times the overall probability of getting the same color from both detectors must be at least 5/9. This is the famous Bell's Inequality:

Probability of getting the same color from both detectors > 5/9

This result follows from our experimental knowledge that we are using a source which always emits pairs of electrons with the same instruction sets (i.e. which always give the same result if the detectors are pointed the same way), but it doesn't assume anything else about the source. For some sources the probability might be 5/9 (e.g. if it always gave the instructions "green for 2 or 3 and red for 1"), it might be 1 (e.g. if it always gave the instructions "red"), or it might be somewhere in between (if it gave different instructions to different pairs of electrons).

V. The Results

So now we are ready to look at the experimental results. This experiment has been done, and the two detectors flash the same color less than 5/9 of the time! In fact it happens 1/2 of the time. Of course the result depends on the source you use, but what I am saying is that there are sources which give this result, whereas we just concluded above that no source could possibly give a result less than 5/9. (Actually the details of this experiment as I've described it are not precisely what has been done in the lab, but exactly equivalent experiments have been done in the sense that our entire analysis above applies equally well to them, and yet they give the result 1/2 in the end.)

If this result doesn't strike you as odd then try to review the argument given above, that the probability would be at least 5/9. See if you can spot any flaw in the argument. We've just come to the main result of the paper, the one which shocked the physics community and which Einstein himself was convinced couldn't possibly happen, and it won't do you any good to know it unless you are clear on why we didn't expect it.

So if you have convinced yourself that the argument was sound, and yet the result it predicted was incorrect, the only thing left for you to conclude is that one of the assumptions of the argument must have been wrong.4 What assumptions did we make? Well, we didn't assume much, but we did assume that once the electrons left the detector they couldn't influence each other in any way. Try and look back at the arguments we made, remind yourself of how this assumption got into them, and think about what would be different if we didn't make it.

The whole notion that the electrons had fixed "instruction sets" was forced on us in order to explain the fact that they always gave the same result if the detectors were pointing the same way. If the electrons can communicate, however, then it's possible that as soon as you measure one of them, it changes the properties of the other one. Just to make up a simple example of how that could happen, imagine that you put detector A in some orientation i (where i is either 1, 2, or 3). Whatever result you get is instantly communicated to electron B, which now changes its instruction set to say it should give that same result if detector B is in orientation i, and give the opposite result in either of the two other cases. If there were some physical law that said that every time you measured an electron it changed the other electron's properties in this way then the two detectors would give the same result only 1/3 of the time, i.e. only when the two detectors pointed the same way. The point of this example (which is clearly not what was actually happening since our result was 1/2 and not 1/3) was simply to illustrate that once you drop the assumption of locality, i.e. the assumption that events can not affect each other instantly at a distance, a probability below 5/9 is possible. The explanation is going to look pretty strange (One electron reaches out across space and changes the other's properties!?), but you can at least construct one. If you want to hold on to locality, however, you just can't get away from the 5/9 limit we derived above.

VI. Conclusions

We have just seemingly disproven one of the great pillars of science, namely the idea of locality. You certainly shouldn't take my word for such a dramatic conclusion. Go through the argument and try to see if you can identify any other assumptions we might have made. Many people have tried this, but nobody has come up with any plausible candidates.5 It seems that once you accept locality, the fact that the two detectors always give the same result when pointing in the same direction forces you to accept that the electrons have a fixed set of properties ("instruction sets") as soon as they leave the source (i.e. at the last moment they are in contact with each other), that these properties are the same for both particles, and that they don't change between the emission and the detection. If any of these conclusions weren't true, but locality was, you just couldn't get the same result every time the two detectors were lined up. Once you accept those conclusions, the mathematical arguments are simply incontestable.

Nonetheless, we have not explained our result. It's one thing to say the electrons must affect each other instantly, but you might still wonder how an electron here instantly knows what is happening millions of miles away. Moreover, in order to explain the results we got, we had to say that the measurement of one electron somehow changed the other one. Why should the electron, either one, be affected at all by my measuring it? My intent was simply to measure a property of the electron, not to change it. This result demonstrates one of the other strange results of modern physics, which is that the act of measuring a property always changes the system you are measuring. In this case the "system" apparently includes not only the electron you are measuring, but also the other one which isn't even there at the time. Physicists have been trying for over fifty years to understand these results, and there is no consensus on how to interpret them. There is clear agreement, however, that the results occur. Spooky action at a distance is part of nature.

Appendix I. Bell's Theorem and Relativity

For anyone who knows anything about Einstein's theory of relativity this result should be particularly disturbing, as it was to Einstein himself. A key notion of relativity is the idea that nothing can communicate with anything else faster than light. If this were to be violated the whole structure of relativity would be in jeopardy. Before abandoning relativity, however, we should look at little more closely at what it means to "communicate." This problem will only arise if somehow I can send a message to someone faster than light.

Let's imagine that we run the experiment with the two detectors millions of miles apart, so that it would take light several minutes to get from one detector to the other. Now let's say I go to detector A and my friend Mary goes to detector B, and we arrange things so that my electron will reach me a fraction of a second before hers reaches her.6 Before going to our respective detectors Mary and I make the following agreement. I want to send her a message from my detector to hers. Maybe there will be something down at my end of the solar system which gives me a hot stock tip, and I want her to have it several minutes before everyone else gets it, so I reason as follows: If I want her to buy I will set my detector to orientation 2. If I want her to sell I will set it to orientation 3. We know that when my electron gets measured those results must instantly change the results she will get from her experiment, so she can figure out which one I did and act accordingly, and we'll be filthy rich.

Can you spot the flaw in this plan? Suppose Mary puts her detector at orientation 2. She will find that half the time it will show red and half the time green, regardless of where my detector was pointing. She will likewise find this same result with her detector at orientations 1 or 3. The problem is that Bell's theorem only deals with how often the detectors show the same result. This doesn't tell her anything until and unless she already knows what result my detection gave, i.e. red or green. Since she can't know that unless I somehow tell her, e.g. by sending her a light signal, there is no way she can know anything about what choice I made with my detector. The only way to see the effect of Bell's theorem is to get together afterwards and compare our results. Then and only then will we be able to see that our coincidence rate was only 1/2, and thus conclude that our electrons were somehow affecting each other.

If you are like me, you will probably find that this explanation is still unsatisfying. We are saying that the electrons seem to communicate faster than light, but somehow relativity is saved because as a technical matter we can't tell that it happened until later. Nonetheless, satisfying or not, Bell's theorem has been experimentally tested and showed that locality must fail, and at the same time relativity has been repeatedly tested and always worked, so until someone comes up with an explanation which shows more naturally why these two results should both be true, we seem to be stuck with getting off on this technicality.

Appendix II. What's Being Measured

There are many ways to measure Bell's inequality. The actual tests which verified it were somewhat different from what I describe here, but the one I am describing is simpler to talk about and quantum mechanics predicts the same behavior for the system of electrons and the property I talk about as for photons and their polarization property, and numerous other systems which can in principle be used to test Bell's Theorem. In this example, however, the property is what's called "spin." If you're not familiar with quantum mechanics, then the simplest way to think about spin is to note that electrons, like many other particles, are small magnets with a measurable north and south pole. The direction of the spin can be identified as the direction of the south pole of the magnet. What the detector is doing is measuring the magnetism of the electron in a particular direction. Classically, you would expect this to give a whole range of results. For example, if I measured the magnetism in the "up" direction then I should get anything ranging from some maximum value if the spin is pointing straight up, to zero if it is pointing to the left or right, to negative my maximum value if it is pointing straight down. But in fact, what quantum mechanics predicts—and experimental results verify—is that no matter what direction I measure the spin of the electron in, I always get exactly +S ("up") or -S ("down"), where S is a number which is the same for all electrons (9.27 x 10-24 Joules/Tesla if you care). This property of spins is just one more strange result predicted by quantum mechanics.

A detector which measures the direction of a particle's spin is called a Stern-Gerlach analyzer, after the two men who first tested some of the quantum mechanical properties of spins. It turns out that measurements of spin yield many bizarre and interesting properties. For example, as I mentioned in the body of the paper, successive measurements of the same electron by detectors in orientation 1 will yield the same result. If the first detector flashes green then the second one will too, but a subsequent measurement by a detector in orientation 2 might flash green or red. Strangely, however, if I then measure the electron with another orientation 1 detector I will not necessarily get a green flash. Measuring its orientation 2 value somehow erases its orientation 1 value!

The quantum mechanical way of viewing this result is the following: An electron always has spin in a particular direction, e.g. straight up. When I measure its spin along an axis I get the result that it will always be pointing directly up or down along that axis. Thus we say that by the act of measuring the electron on a given axis I actually change the electron's spin, forcing it to line up on the axis I chose. Given this I can explain the results cited above. If I measure the electron in orientation 1 and find it pointing up then its spin will subsequently be aligned exactly in that direction. Thus further measurements along orientation 1 will give the same result, i.e. "up". If I then measure the electron along orientation 2, however, I will force it to point one way or another along that new axis. This is what I mean by "erasing" the orientation 1 value. Since the electron now points up or down along orientation 2 a subsequent measurement along orientation 1 may yield either result, up or down. (For the details of how to calculate the odds of each result see the following appendix.)7

This effect, strange as it may seem, is exactly the kind of thing we found we needed to explain the failure of Bell's inequality. We've just seen that measuring the spin of an electron changes its state by forcing it to be aligned along the direction we measured in. The additional element we need to get around Bell's inequality is that the measurement of one electron changes the state of the other one. This comes about because of a special property of the sources which emit the electrons. The two electrons in each pair are linked ("entangled" in the lingo) in such a way that when I measure one electron to be pointing in a particular direction, the other electron will be forced to point the opposite way along the same axis. If I measure one electron in orientation-1 as "up," then the other electron must point "down" in orientation-1; and both electrons will be unpredictable if measured in any other orientation.8 This effect gives us the violation of locality needed to invalidate the proof of Bell's inequality. For more details on how this works, and how specifically you get the result 1/2 for the experiment, see the following appendix.

The effect of measurements on a system is one of the most profoundly shocking results of quantum mechanics. Put succinctly, measuring a system necessarily changes the system. We see this effect with any measurements of spin, but it comes out even more dramatically in Bell's theorem, where measurement of one electron necessarily must somehow be changing the other electron. Nobody understands how this happens, but experimentally we can say that it does.

Appendix III. The Calculation

This appendix is intended to fill in a little detail on the calculation of the number 1/2 which I said was the actual result of the experiment described above. I am not going to derive this result from the fundamental principles of quantum mechanics, but rather state without justification the results of measuring successive spins and show how these rules give rise to the number 1/2 in the circumstances described above. There will be a little more math here than in the rest of the paper. Moreover the last part of this appendix talks about how to view this calculation from the standpoint of relativity, and this section may be confusing to readers who are unfamiliar with relativity theory. However, nothing in this appendix should be necessary for understanding any of the rest of the paper, including the other appendices.

Recall that when you measure an electron's spin in one direction you erase all information about the electron's spin in any other direction. By this I mean the following: If I measure the spin in the left/right direction I will always find it pointing exactly left or exactly right. Say I measure it pointing left. If I measure it again in the left/right direction then I will definitely see it pointing left again. If I measure it in the up/down direction, however, then I will have 50/50 odds of seeing it point either way. Once I do that measurement, however, I will have fixed it to be pointing either up or down, and a left/right measurement will once again yield 50/50 odds. What if I measure it in some intermediate direction between up/down and left/right? The formula, which I will not derive here, is that if an electron is pointing in a particular direction and you measure its spin in another direction which is some angle q away from the first one (see diagram) then the probability of finding it pointing in that direction is cos2(q/2).

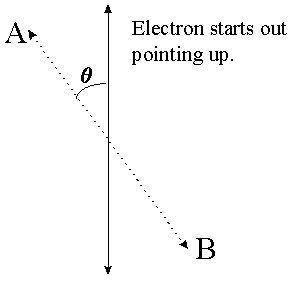
Theta is the angle between the previous measurement and the current measurement

A measurement in the A/B direction will yield "A" with probability cos2(q/2), and "B" with probability 1-cos2(q/2), i.e. sin2(q/2).

So let's examine the experiment described above using these rules. Let's say I emit two electrons and detector A measures the first one in direction 3. Since we don't know anything about the electrons' spins yet there is a 50% chance I will see a green light, indicating that the electron is pointing in direction 3, and a 50% chance I will see a red light, indicating that the electron is pointing directly away from direction 3. Note that these are the only two possibilities. After a measurement in a particular direction the electron will always be pointing exactly towards or away from that direction.

Let's suppose that we get a green light, so we know electron A is pointing in direction 3. Because of the way the electrons are entangled we now also know that electron B is pointing directly away from direction 3. This is where the spooky action at a distance comes in. The fact that we chose to measure electron A in this particular direction not only affected that electron, it also forced electron B to be pointing exactly towards or away from this direction! So what results do we get at detector B? If detector B is set to position 3 then it will definitely flash green. (Remember that green means opposite things at the two detectors.) If detector B is set to position 1 or 2 we have to use the cosine rule given above to find the probability of it flashing green. Since the three directions are each separated by 120o, the probability of getting a green flash in either of these other two positions is cos260o, or 1/4. The total probability can be calculated as follows: 1/3 of the time detector B is in position 3 and it necessarily flashes green. 2/3 of the time detector B is in position 1 or 2 and flashes green with probability 1/4. So the total probability of detector B flashing green is: Probability = 1/3 (1) + 2/3 (1/4) = 1/2. Once again the most important part about this result is that it relies on the two measurements affecting each other, which is why it is not constrained by the 5/9 limit derived above.

Readers familiar with relativity may be disturbed that this derivation assumed that detector A measured its electron first. According to relativity theory it's meaningless to say which measurement happened first. Some observers will say measurement A happened first while others will say measurement B came first, and they will both be equally valid viewpoints.9 This doesn't affect the results of this calculation, however. If you redo the calculation from the point of view of an observer that says B came first you will get the same results, namely that if both detectors are pointing the same way they will give the same result every time, whereas if they are pointing different ways they will give the same result 1/4 of the time.

Once again, we find relativity is saved by a technicality; but this one is even more disturbing than the last one (in Appendix I). From one point of view the measurement at detector A happens first and instantly changes the state of electron B. From another point of view the measurement at detector B happens first and instantly changes the state of electron A. Physically these descriptions seem completely incompatible. Surely one of them must be the "correct" interpretation of what happened. Yet experimentally there is no way to distinguish between the two interpretations, so relativity can safely say that either one is a valid description from some particular point of view.

Because I find this result so remarkable and incomprehensible, I think it bears repeating. In order to explain the failure of Bell's inequality we had to conclude that one of the measurements (presumably whichever one happened first) affected the state of the other electron. Yet relativity tells us it is a matter of perspective which measurement was the cause and which the effect. Although we can't ever distinguish these two perspectives experimentally, the idea that they should both be valid seems to bring into question some of our most fundamental views about causality. Issues such as these which arise in trying to reconcile relativity and quantum mechanics are, in my opinion, among the most fascinating aspects of physics.

"There are more things in heaven and earth, Horatio,
Than are dreamt of in your philosophy."
-William Shakespeare

Footnotes

1. In the final appendix I will add and multiply fractions and take a cosine. This appendix is unnecessary for the rest of the paper and can be skipped without any loss of continuity.

2. N.D. Mermin, "Bringing Home the Atomic World: Quantum Mysteries for Anybody," Am. J. of Phys. 49(10), p. 940, Oct. 1981.

3. I am actually cheating a little here, because in the real experiment the results are always opposite rather than always the same. This is a detail which doesn't affect the argument in any way, but it's easier to talk about them being the same. The simple way around this is to cross the wires at detector B, so that whenever it measure a response which would have caused it to flash green it now flashes red and vice-versa. By putting oppositely wired detectors like this on the opposite sides of the room you can get them to always flash the same color for a given pair (assuming of course that the two detectors are still oriented in the same way).

4. It might occur to you that since we are talking about probabilities of how often we should get particular results, the outcome could in principle be a coincidence. Maybe the two detectors do tend to give the same result 5/9 of the time but just happened to be the same 1/2 of the time in our particular experiment, just by random luck. In practice the number of particles involved is so huge that the probability of such a spurious result is small enough to make winning the lottery seem like a sure bet by comparison.

5. I know of at least one published claim to have found a loophole in the argument here: Hess and Philipp, "A possible loophole in the theorem of Bell," Proceedings of the National Academy of Sciences USA, Vol. 98, Issue 25, 14224-14227, Dec. 4, 2001. In my opinion the mathematical argument in this "loophole" is flawed.

6. Those who know some relativity can insert the phrase "in our shared reference frame"; those who don't can ignore this footnote.

7. Technically speaking I'm cheating a little here by equating spin with magnetic orientation and then saying it always points exactly in the direction you measure it in. When the spin of an electron is measured to point left this actually means the magnetic south pole of the electron is a little bit off from that direction. This detail, although necessary for certain kinds of calculations in quantum mechanics, is irrelevant to the discussion in this paper.

8. Note that since a measurement of one electron forces the other to point in the opposite way, I would normally expect that if I set both detectors to position 1 they would always give opposite results. This is why I said earlier (in a footnote) that the wires at one of the detectors should be crossed, so that if detector A flashes green when it sees an electron pointing in some direction then detector B should flash red for that result and green for the opposite one.

9. This statement about the order of events being relative is only true for events which are sufficiently far away in space and close in time that a light signal wouldn't have time to go between them. The two measurements in this experiment must be set up like that, otherwise you could just imagine that the electrons communicate by sending a signal and there would be no need to invoke spooky action at a distance.

Gary and Kenny Felder's Math and Physics Help Home Page
www.felderbooks.com/papers
Send comments or questions to the author