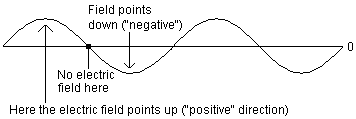
Copyright (c) 1998 by Gary Felder and Kenny Felder
In this paper, we attempt to explain some of these fantastic notions for the layman. This paper comes with a warning, but also with some good news. The good news is that you don't need to be majoring in physics or take several weeks in a course to learn about this. What physics students spend most of their time learning is a set of mathematical tools for doing calculations. We are not going to get into the math at all here, but just present some basic experimental results and the ideas developed to interpret them. The warning is that it's not going to be easy. We are going to introduce some of the most conceptually difficult ideas in science, and we're going to cover several weeks worth of college physics. You might go through the whole paper once fairly quickly, but don't necessarily expect to get the whole thing in one sitting. Try reading it in stages and stopping when you feel you've got enough to chew on. After ruminating for a while come back and try the next bit. The main point is not to expect to get everything instantly, but just to relax and give yourself time to think and absorb it all. And—hopefully—to enjoy it!
The first sections are all explanations of "classical" Physics: that is, the understanding of the 19th century world, before the introduction of quantum mechanics. These provide a critical background for understanding the 20th century changes. Don't skip or skim them "to jump to the good stuff" because without this background, the good stuff won't make any sense!
Then we jump into the 20th century, and quantum mechanics.
At any given point in space, there is something called an "electric field." No one knows exactly what it is, but we do know it has an effect, which is that it pushes charged particles around. So for instance, we might say that at this exact spot, the electric field "points up." That means if you put a positively charged particle there, it will be pushed up.
We could go on for hours about electric fields and charged particles and all that good stuff, but it wouldn't really be relevant to this discussion. The important thing to know is that, under the right circumstances, you can wind up with an electric field that alternates as follows. At some given point in space, there is an electric field pointing up. A little to the right of that, no field at all. A little to the right of that, the field points down. And then back to zero, and so on, oscillating up and down. You can make a plot of this field, and it will have a "sine wave" shape like this:
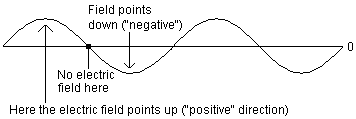
The way to understand this picture is to remember that the horizontal direction shows where you are in space, and the height of the curve shows the strength and direction of the electric field at that point. Nothing is actually physically moving up and down, this whole picture takes place along a line.
But there is one more wrinkle, which is that the wave is moving. Picture that whole drawing moving, at a constant speed, to the right. So if you stood just in one spot and measured the electric field where you were standing, you would see it pointing up, then down, then up, then down, as the wave flowed past you.
One of the greatest accomplishments of 19th century Physics was to show that you can describe an alternating electric field moving through space, and explain almost all the observed properties of light with this one simple picture. (Actually light also involves something else called a magnetic field, but it's not particularly relevant to what we are discussing.)
Before we go on we need to introduce a piece of terminology which will be helpful later. The distance from one wave-top to another is called the "wavelength," and different light waves have different lengths.
If you are an experimental type, you might immediately run off and shine two flashlights at the same spot on the wall, to see how they add. Unfortunately, a flashlight beam is a chaotic mixture of many different light beams with different wavelengths, so you won't really see much of anything except a big blur on the wall. But suppose you had a couple of special flashlights that could emit one simple in-phase electric wave each, with exactly the same wavelength? Pointing these two flashlights at the wall, you would discover them adding up in a pretty surprising way. Depending on where you held them—specifically, depending on their distances from the wall—they might create a bright spot, or they might create nothing at all! This is because of a "phase difference" which is pretty easy to understand if you draw it.
In the picture below, you see two identical "in phase" waves, representing the light waves from the two individual flashlights. When one has a positive electric field, the other has a positive electric field: so they add up to a very high electric field. When one is negative, the other is negative: so they add up to be very negative. The result is a new wave which is taller than the original two waves. Light plus light equals brighter light.

If they are "out of phase" then the opposite happens. When one points up, the other points down, so they consistently cancel each other out. The net result is no electric field at all, anywhere. Light plus light equals darkness.
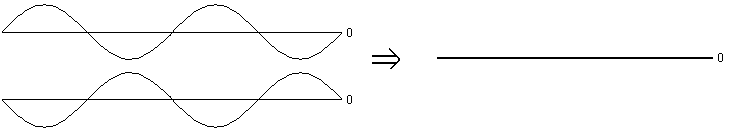
If you'll forgive the introduction of a bit more fancy terminology, these two situations are referred to as constructive interference (both waves point the same way, so they make a bigger wave) and destructive interference (the waves point opposite ways, so they tend to cancel each other out).
So let's go back to our magical-same-wavelength-in-phase-flashlights-shining-on-the-wall. If the two flashlights are exactly the same distance from the wall, they are in phase—they hit the wall exactly the same way, so the spot where they hit lights up. Move one flashlight back by half a wavelength, and now they are out of phase—one hits the wall "up" when the other hits it "down" and vice-versa—so the wall stays dark. Move it back another half wavelength, and they are back in phase, and the wall is lit up again. Move it back less than half a wavelength and you get something in between, where the wall is lit up less brightly than the in phase spots but is not completely dark.
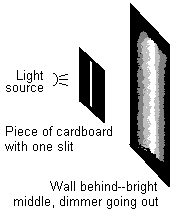
Sounds pretty cool, doesn't it? Unfortunately, that experiment in that form would be practically impossible to do. But a man named Thomas Young came up with a very clever way to fake it, using only one light source. It still needs to be a pretty special light source, with one consistent wavelength—in other words, don't try this at home! But it can be done in the lab, and it provides one of the best experimental vindications of the wave theory of light.
Well, if light always traveled in a simple straight line, you would just see a small vertical bar of light on the wall. But light actually radiates outward as it travels. So the light goes through the slit, and then starts radiating outward. What you see on the wall is a very bright bar immediately behind the slit, and then dimmer light—but not none!—to the right and left of the slit.
OK, that's not the most interesting result in the world. It does seem to confirm the radiating outward idea, but what about all the wave stuff? Well, where things get really interesting is when you add another slit to the cardboard. You might expect to see the same pattern we saw the first time, only repeated twice: two bright vertical bars, getting dimmer the further you get from them. But in fact, what you see is a new pattern. Bright bars where a lot of light is hitting the wall, alternate with dark bars where no light seems to hit at all.
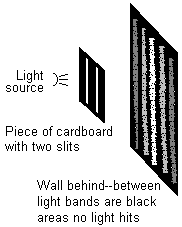
This seems really odd at first—some of the places on the wall that were lit up in the single-slit experiment, have become darker just because you opened a second slit! Put your hand over the second slit and suddenly those spots get brighter again. This makes perfect sense in view of the wave theory of light, though. Remember that when one little tiny beam gets through a slit, it immediately spreads out in all directions. So for any given spot on the wall, there are two beams of light hitting that spot—one from each slit. You can see this in the diagram below, which is looking straight down on the previous diagram.
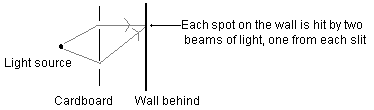
Now, what do you see when you look at that spot on the wall? The two waves started out identical, but they have traveled different distances (for the particular spot in the drawing, the top path is much shorter than the bottom), so they are at different points in their cycle. If both are "up" or both are "down" then you get a very bright patch—the two beams of light constructively interfere, creating more light than either one individually. But if one is "up" and the other is "down" then you get a dark patch—the two beams of light destructively interfere, actually canceling each other out.
Slightly further down the wall, the top path is a bit longer, and the bottom path is a bit shorter. So the interference is different: if it was constructive before, it may be destructive now. And so on, up and down the wall. This explains the alternating light and dark bands, which are therefore referred to as an "interference pattern."
Then, before we go on to more hard stuff, we're going to take a break and look at something much easier (and more fun): we're going to repeat the experiment with M&Ms.
We'll start with the single-slit experiment. Instead of a light source, we have an M&M-throwing-machine. Each M&M is covered with white ink so that it leaves a stain on the black wall behind (since, as we all know, the milk chocolate only melts in your mouth). You set your M&M-throwing-machine going, it throws out a ton of M&Ms one at a time, and then you look at the ink pattern on the wall—this will tell you where the M&Ms hit. What do you see? Well, the machine is just mechanically spitting out M&Ms in the same way every time, so of course there is just one spot on the wall, where they all hit. M&Ms, unlike light, don't radiate outward in all directions: they just follow a single course to a single destination.
So that wasn't much fun. Let's mix it up a bit: say, stand behind the M&M machine and rattle it around a lot, so the M&Ms get thrown off in all directions. Now, a lot of them bounce off the cardboard. The ones that get through tend to hit the wall near the slit, but not all right behind the slit. So, after enough M&Ms hit, you get a result very much like the single-slit experiment with light: a big white bar that gets dimmer as you move out.
Now, let's add a second slit and do it again, still throwing M&Ms at random angles. What do you see this time? Are there alternating bands of white and black? No, certainly not. Since we are throwing the M&Ms one at a time, what you will see is all the ink from M&Ms that went through the left slit, and all the ink from M&Ms that went through the right slit, added together. So there aren't any bands that suddenly go dark. There's a big white bar behind each slit, and it gets darker as you go away from the slits.
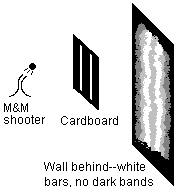
(Note from our lawyers: the authors of this paper accept no responsibility for the consequences if you attempt to repeat this experiment at home.)
19th century Physics viewed everything as either a wave or a particle. Waves are things like water waves, or sound waves, or light waves. Particles are things like golf balls, molecules, planets, and bite-sized chunks of hardened chocolate liquor in a delicious crunchy shell. Sometimes a wave is made up of particles, as for instance when you make standing waves by shaking a rope. But regardless of what they are made of, waves and particles act very differently. Some of the differences are:
OK, that metaphor didn't quite go the way we were hoping. Sorry about that.
But the turn of the century saw some annoying experiments, and even theoretical problems, that couldn't quite be explained away. In an ideal world, we would now explain these new experiments in detail. But unfortunately, that would take another whole paper or two, so we're just going to tell you the outcome.
In 1905 Albert Einstein made a proposal, described below, which explained all the known experimental data about light, as well as making some new theoretical predictions. These predictions, involving an experiment known as the "photoelectric effect," were subsequently verified to high accuracy by Robert Millikan. (It was for this proposal, and not for the theory of relativity which he also proposed in 1905, that Einstein was eventually awarded the Nobel Prize.) The proposal was that light can be viewed as a particle. A beam of light is a collection of discrete particles which Einstein called "photons." If you turned on your flashlight for a minute and then turned it off again, you could in principle say that you had emitted exactly x number of photons. (In practice this would be difficult to figure out since the number would be very large, but it would be pretty easy to come up with a good estimate.) Einstein showed that you could very simply explain some already known puzzling results as well as correctly predict the results of the photoelectric effect with just this one idea.
This result presents us with a serious problem, though. The double slit experiment seemed to show conclusively that light was a wave. Light produces an interference pattern which particles, such as M&Ms, don't. Long before Einstein, this fact was taken as a clear refutation of the idea that light beams are made up of discrete particles.
So now we have experimental evidence (the double-slit experiment) that light is a wave, and other evidence (the photoelectric effect) that light is a particle. You may think that you can have it both ways by saying light is "a wave made up of particles" (like water waves), but as we will explain below, this explanation doesn't work. Or you may object that we haven't given you any reason to believe in this particle theory of light since we never described the effects, such as the photoelectric effect, which it was used to explain. We're going to do something even better. We can use the double slit experiment itself to prove that light is made of particles, and at the same time, to show the serious contradictions that we face when we try to describe light as both a wave and a particle at the same time. In the flames of this burning contradiction, quantum mechanics will be forged before your very eyes.
What we're going to do, in this section, is the double-slit experiment with a twist. Use a very, very dim source of light; and replace the back wall with a photographic plate, monitored by a computer. The result is that at any given moment, very little light is hitting the wall; but the computer can tell you exactly what light hit where, when. And over time, the photographic plate will become a permanent record of all the light that has hit it. When you do the experiment this way, you find that one little point of light is hitting the wall at a time. A little blotch of light here, then a little blotch of light there, with a small but measurable delay between them, and the "pattern" on the wall emerging only after many different blotches have hit. In a pure wave theory of light, this result would be baffling. But with our new particle view, it makes perfect sense: we see that we are actually shooting out, and measuring, one photon at a time. Thus, the double-slit experiment actually proves the particle theory of light. But, as we warned earlier, the consequences can be very disturbing when you look in more detail.
Start with the single-slit experiment. You shoot one photon, it goes through the slit, and it hits the wall. It doesn't leave a "pattern" of any kind, just one little blotch. The next photon hits someplace else, leaving another blotch. After a lot of photons have hit the wall, a pattern starts to emerge, and it is the familiar single-slit pattern. There is a bright white bar behind the slit, where a lot of photons hit—and then, as you move away, it gets dimmer, because fewer photons have hit. So overall, the photons seem to be acting like particles: the results are the same as they were in our experiment with a randomized M&M shooter. But of course, we already knew that the single-slit experiment yields basically the same result with both particles and waves, so we haven't really learned much here.
The interesting stuff comes, of course, when we try it with two slits. Once again, we see one photon blotch, and then another, and then over time a pattern emerges. But is it the characteristic "particle pattern" or the "wave pattern"? The answer is, it is the wave pattern: bands of light (where a lot of photons hit) alternate with dark bands (where very few photons hit). This makes sense if you remember that the photons are actually the components of light. So this is identical to the original double-slit experiment with light, only slower.
But there is a deep theoretical problem here that you may have spotted. Why did we get dark bands? The original explanation was that the light from one slit was interfering with the light from the other slit, effectively canceling each other out at those points. That made sense because light was continually streaming through both slits. In this case, only one photon has gone through at a time—so what could have interfered with it? [This is why it doesn't help to say light is "a wave made of particles." Waves show interference patterns because one part of the wave (that went through the first slit) interferes with another part (that went through the second slit). Once you do the experiment one particle at a time there doesn't seem to be anything left to make an interference pattern with.]
Please pause for a second, because we are—right now—at the most crucial point in this paper. Everything hinges on your ability to understand how utterly nonsensical this result is. To fully appreciate this, put yourself at one spot on the wall, during the single-slit experiment. Most of the photons get blocked by the cardboard, but once in a while, one comes through, and hits the wall. Occasionally a photon hits the wall right where you are.
Now, someone comes along and cuts another slit in the cardboard. Nothing else in the experiment changes. But after a while, you start to notice that no photons are hitting your spot on the wall any more—ever—from either slit. You are apparently on one of the "dark patches." It wasn't dark with only one slit open, but it is dark with two slits open.
Why are no photons hitting this spot any more? Have they stopped going through the original slit entirely—just because a new slit was opened? Or are some of them still going through the original slit, but they aren't then going to your spot—again, just because a new slit was opened? Neither answer makes any sense, and yet it seems that one of them must be true.
Instead of trying to resolve this dilemma with a theory, let's try to solve it with an experiment. We put a measuring device by each slit, that will record when a photon goes through the slit. This way, when a photon hits the wall, we will know which slit it went through, and we can determine if opening up the second slit actually reduced traffic through the first slit, or redirected it. What do we find? Something entirely unexpected—the wave interference pattern is gone. Instead, we just see a simple particle pattern on the wall, with bright bars that get dimmer. There are no dark patches. It doesn't matter how we do the measurement, the result is the same: when we don't know which slit the photons are going through, we get a wave interference pattern. When we do know which slit each photon traveled through, no interference pattern. We will discuss this result in more detail below, but right now we just want to stress that this is not a theory, it's an experimental fact which has been verified many times. Sensible or not, measuring the photon's path changes what it does.
So those are the experimental results. This would be another good time to back up, maybe re-read the section, and think it over. The results are true. Do you understand why they seem paradoxical? Can you find a good physical theory that might explain them?
We have to proceed cautiously here. We have some very odd results, and in order to explain them, we're going to need to come up with some radical new ideas. So we want to make sure that our conclusions are grounded very firmly in the data. Before we come up with any grandiose theories, let's make as many observations as we can about the experiments.
One of the first observations we can make is that, except when we measured each photon coming through a slit, this one-photon-at-a-time experiment yielded exactly the same results as the normal light experiment. So we are led to propose the "Correspondence Principle" which states that if you take enough photons, and measure them en masse instead of one at a time, they act exactly like light—which is not surprising, since they are light! More generally, the Correspondence Principle states that classical Physics works, and makes the correct predictions, as long as you don't look at things in too fine detail. This is very important because we have to take into account the fact that, by and large, classical Physics did such a good job of predicting things!
Another important observation is that when we did our first M&M experiment, we got just one spot on the wall—all the M&Ms went to the same place, until we started shaking up the throwing device. But in the case of the photons, we didn't have to shake anything. The light source did exactly the same thing every time, but the photons didn't all hit in the same place. In fact, they couldn't possibly all hit in the same place, or we wouldn't get a pattern on the wall, and the photons would not be behaving like light waves! This forces us to one of the most uncomfortable conclusions of quantum mechanics: you can set up a situation in which the initial conditions are exactly the same, and get different results. In other words, there is true randomness in the universe. We can predict statistically where a photon is likely to go (based on the patterns that emerge), but not where an individual photon will go.
(It might occur to you to wonder if the initial conditions are really the same. Maybe there is really something different about the photons which makes them go to different places, even though the light source does the same thing every time as far as we can tell. This kind of idea is called "hidden variable" theories since it assumes that the photons' paths are determined by some properties which we can't measure, but which make the initial conditions different each time. While it's an appealing idea, most physicists feel that these theories can not satisfactorily explain the data, and that quantum mechanics does imply true randomness.)
If you take those two observations—the Correspondence Principle, and randomness—you can start to pull it together just a bit. Consider throwing dice. One individual die is unpredictable. It could be a 1, or a 3, or a 6, who knows? But when you throw millions of dice, you can confidently predict that the average will be 3.5. So the Correspondence Principle says that classical Physics worked, because it was always dealing with aggregate properties of large numbers of particles (photons, dice) and could make correct predictions. But those predictions and theories don't apply at all to individual particles which may follow very different rules.
At the same time, we have to stress again, there is a fundamental difference between the randomness of a die and the randomness of a photon. The throw of a die isn't "really" random. If you knew everything possible about the angle it was thrown at, and its weight distribution, and the table it was landing on, and so on, you could in principle predict its flight perfectly and tell what number will come up on top. But in the case of the photon, it doesn't matter how much you know up front: because even when all the starting conditions are the same, it may do different things. (Of course the die is really made up of tiny particles obeying quantum mechanics and displaying true randomness, but there are so many of them that the overall behavior of the die can in principle be predicted with near certainty.)
Anyway, let's get back to our experiments. What other observations can we make? One of the things that was most disturbing about the double-slit experiment was the fact that opening the second slit prevented photons from going through the first slit to some spots on the wall. It seems impossible to avoid the conclusion that, even when a photon went through the first slit, something also traveled through the second slit, and interfered with it. In fact, since we got such a perfect wave interference pattern, it's very tempting to conclude that some wave went through both slits and interfered with itself. But what wave? It can't be a light wave—we only shot one photon, and (by definition) it is the smallest possible unit of light, so it cannot split into two light waves. Put another way, if the light wave were spreading out and going to both slits at once, we would expect it to also hit more than one place on the back wall at once. Since we measure only one hit we conclude that a single particle is coming through. So some other sort of wave seems to be involved, a wave that goes through both slits when there is only one photon.
Finally, one more observation: when we measured which slit the photon went through, the results of the experiment changed. You can measure it many different ways, and you still do not get an interference pattern as long as you are detecting which photon goes through which slit. Measurement matters.
This particular result is so important and so contrary to our classical notions of the world that it bears repeating. In classical physics things are assumed to happen in the world the same way, whether we look at them or not. Of course you can disturb a system by measuring it in some particularly clumsy way, like feeling around with a large stick to figure out the position of a Ping-Pong ball. But if you are careful enough, you can do your measurements in such a way that they barely disturb the system at all, and it continues to act as it would have without you there. But in the double slit experiment there is no clean way to separate the experimenter from the experiment. No matter how you do the measurement, the simple fact of measuring which slit the photon goes through causes the interference pattern to disappear.
The ideas we're going to describe have been formulated in a number of different ways. These are equivalent from a strictly scientific viewpoint, meaning they predict the same results from experiments. They differ, however, in how they interpret the results. Since you can't use any experiments to decide between these interpretations, any choice of one over another is at most an aesthetic choice. Nonetheless there is one conventionally agreed upon formulation which most physicists use when they talk about quantum mechanics. This formulation, developed primarily by Niels Bohr and known as the "Copenhagen Interpretation," is the one we will follow below.
We've already said that some new kind of wave seems to be involved. We can't explain really what it is, but we can do the next best thing, which is give it a fancy name. We call it a "wavefunction." It is commonly represented by the Greek letter Y (spelled psi, pronounced like "sigh," and for good reason).
When you fire your photon emitter, what actually comes out is a Y wave (ie a wavefunction). It is not random: it travels according to the perfectly predictable laws of wave propagation, moving out in all directions and interfering with itself and all that good stuff. According to the Copenhagen interpretation, the Y wave represents the probability of the photon being at any particular place. So at this stage, the question "Where is the photon?" does not have an answer—there is only a wave of probabilities traveling outward.
In terms of the math, we can represent Y with a drawing very similar to the drawing we used for a light wave at the beginning of the paper. But it's important to remember that the drawing means something very different! In a light wave, the height of the drawing corresponds to the strength of the electric field. In a Y wave, the height of the drawing represents the probability of finding the particle at a particular point. To make it more confusing, Y can be negative or positive, but the probability is always positive—the probability only cares how far from zero Y is, it doesn't matter at all which direction! So you might see something like this:
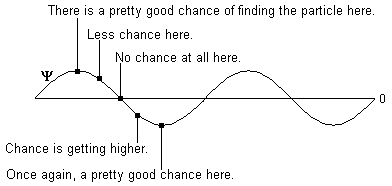
Until you look to see where it is, the photon isn't at one place or the other. It simply has a bigger wavefunction value—a higher probability—in some places than in others. So interference works just like it does for any other wave. In constructive interference, areas of high probability add to give areas of very high probability:

In destructive interference, areas of high probability cancel out to give low (or zero) probability:
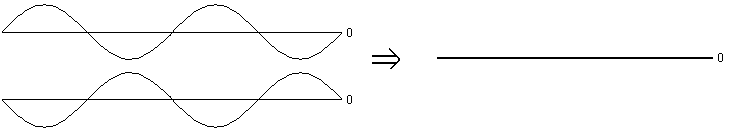
Then, at some point, you actually measure the position of the photon. You can't measure "maybe here maybe there"; a measurement always yields an actual position. So the measurement has the effect of forcing the photon to "choose," based on its current probabilities, where to actually be. In quantum mechanics lingo, your measurement "collapses" the wavefunction—it used to be spread out through space, and now it just says "the photon is definitely right here."
So how does that theory apply to our experiment? First let's look at the original double slit experiment. You shoot out a photon. The Y wave travels from the photon emitter, through both slits, and back to the wall, creating a pattern just like light would, except it's a pattern of probability instead of light. At the back wall (with its photo-sensitive surface) the photon is measured, which collapses the wave function: the photon has to choose where to hit. Of course, lots of photons choose high-probability areas, only a few choose low-probability areas, and none of them choose zero-probability areas. That's why we see the interference pattern.
But when we put measuring devices in the slits, we collapse the wavefunction much earlier. We force the photon to choose which slit to go through: one probability becomes "definitely yes" and the other becomes "definitely no" in that instant. Thereafter, there is only one beam, and hence no interference and no interference pattern.
Take a few minutes to chew on this. You should be able to convince yourself that the Copenhagen interpretation does explain the results of all our experiments. And because Y waves propagate exactly like light waves, it also satisfies the Correspondence Principle: for any measurements of large numbers of photons, quantum mechanics and classical Physics will make the same predictions. This isn't immediately obvious, but if you think about it, and think in particular about the explanation of the double-slit experiment above, we think you'll agree.
To answer this question, we're going to try an experiment with something new. Of course it's going to be the double slit experiment again. (Most experimental physicists do actually perform other experiments too, but they need not concern us here.) However this time, instead of light, we will shoot electrons through the slit. In other words we set up an electron gun firing electrons at the wall with the slits, and on the back wall we have an electron detector which can measure when and where the electrons hit. Just to make sure they aren't bumping into each other, we can shoot them through one at a time just like we did with the photons and M&Ms.
So what do we find? Surely you would expect to see the familiar particle pattern on the back wall, namely a big blob behind each slit and no interference pattern. After all, this experiment seems like it ought to be identical to the M&M experiment we performed above. About 20 years after Einstein proposed his particle theory of light, though, a French graduate student named Louis de Broglie proposed that all particles have wavefunctions. If this is true, then the electron wavefunctions should show interference just like the photon wavefunctions.
As you've probably guessed by now, this is exactly what happens. De Broglie was awarded his Ph.D. for this idea and five years later, when the experiments had been done, he was awarded the Nobel Prize for it. It turns out that you get an interference pattern whether you use electrons, protons, or even entire atoms. In fact, everything seems to do this. What you find, however, is that the bigger the particle the closer together the interference fringes (the vertical stripes on the wall) are. This means it's much more difficult to measure interference patterns with atoms than it is with electrons. And with M&Ms, the fringes are so close together that it looks just like a big blur (which, as you may recall, is what it looked like). Thus we are once again led to the Correspondence Principle. Measurements of big things, roughly meaning anything much bigger than an atom, will seem to produce classical results because the quantum mechanical results (eg interference fringes) are too small to detect.
(Actually the fringes with electrons and atoms are already so close together that they are almost impossible to detect, so the experiment used to show their wave nature wasn't the double-slit experiment but a variation of it using crystals to scatter the particles. We won't describe it here except to say that the effect shows wave effects very similar to those in the double slit experiment.)
But of course, the theory also raises a lot of disturbing questions. To name just a few,
But one thing you can do is think about it, as hard and as long as you can. Look for contradictions, paradoxes, mysteries. Do "thought experiments" where you imagine a situation, and try to imagine what quantum mechanics would predict. Toy with the ideas.
Here is an example suggested by one of the founders of quantum mechanics, Erwin Schrödinger. You set up an experiment where a particle (small enough that quantum mechanical laws matter) has a 50% chance of decaying after an hour. The particle is in a box, and you don't look. After an hour, what is the state of the system? Classically, you would say that the particle has either decayed, or it hasn't, and you'll know when you look. Quantum mechanically, you say that the particle is in an undetermined state—its Y simply says "maybe decayed, maybe not"—and it won't actually decide until you look. The two sound very much alike, but they are different. To make the difference more vivid, you put a cat in the box, with an apparatus that will kill the cat if the particle decays. Now, is the cat in a state of "maybe dead, maybe not," truly an undecided middle ground, until you look?
It sounds as if this conclusion is ridiculous. Or it may sound like this conclusion is meaningless: saying "the cat is half dead/half alive until we check on it" is just a fancy way of saying "the cat is either dead or alive, but we don't know until we look." But remember the experiments we've discussed, and the conclusions we drew. Quantum mechanics says that these two statements are definitively different, and the intuitive one (the cat is either alive or dead, and we just don't know until we look) is wrong. The photon really, genuinely, and importantly, does not have a specific location until we measure one. The cat really isn't alive or dead.
It doesn't seem to make sense. But another school of thought says, why should it make sense? After all, humans evolved in a world of "normal" objects. And we developed a facility called "intuition" that helped us survive in that world, by helping us predict the effects of our actions. That physical intuition was, and is, a great asset. But perhaps it shouldn't be too surprising that it becomes a liability when we try to apply it to areas that we didn't evolve for. Quantum mechanical laws generally only have measurable effects when applied to things that are too small to see, so we never evolved an understanding of them, so they seem bizarre.
In fact, at roughly the same time that quantum mechanics first began to suggest that very small things defy our intuition, Einstein was proposing his special theory of relativity (read about it here) which shows that very fast things defy our intuition; and then his general theory of relativity, which concerns the odd behavior of very big things. It seems that, more and more, the only way to understand the world is to apply the math, and stop trying to "understand" what's actually going on.
But some of us keep trying anyway. That's one of the reasons we wrote this paper...
 Gary and Kenny Felder's Math and Physics Help Home Page
Gary and Kenny Felder's Math and Physics Help Home Page
www.felderbooks.com/papers
 Send comments or questions to the authors
Send comments or questions to the authors