Spectra

The function spectra() calculates several spectra for the output fields. The function begins by performing a Fourier transform on the field and derivative grids, thus generating lattices of Fourier values $f_k$ and $f_k'$. At each gridpoint in Fourier space the function then calculates $\vert f_k\vert^2$, $\vert f_k'\vert^2$, $n_k$, and $\rho_k$. The formulas for the occupation number $n_k$ and the energy spectrum $\rho_k$ are given below.

The spectra() function doesn't output these values for each grid point, but rather groups them into bins. The size of the bins is determined by the lattice spacing $dk$. This means for example that in three dimensions the $0th$ bin ($0\le k < dk$) includes only the point $k=0$ while the next bin ( $dk \le k < 2 dk$) includes the $9$ neighboring points. In one dimension there should be one point per bin. The four quantities listed above are each averaged over each bin.

The output of this function is in several files. The first, spectratimes_ext, simply lists the times at which spectra were recorded. There is also one file per output field that contains the spectra. These files are called spectra$<$field_number$>$_ext. They contain seven columns listing, for each bin, $k$, the number of points in the bin, $\omega_k^2$, $\vert f_k\vert^2$, $\vert f_k'\vert^2$, $n_k$, and $\rho_k$. (The quantities $\omega_k$, $n_k$, and $\rho_k$ are defined below). Note that the four spectra (the last four columns) are calculated at each point on the lattice and then averaged for the bin, whereas $k$ and $\omega_k^2$ are given for the bottom of the bin.

At each time for which spectra are recorded the spectra() function will write one row for each bin into each of the spectra files. When examining the output it's easy to tell where one time ends and another begins because the frequencies (first column) will monotonically increase at each time and then reset to zero when a new spectrum begins.

The number of points in each bin is given to make it possible to take sums of different quantities over the lattice. For example Parseval's theorem for a discrete Fourier transform states

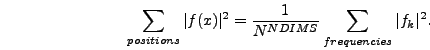$$\sum_{positions} \vert f(x)\vert^2 = {1 \over N^{NDIMS}} \sum_{frequencies} \vert f_k\vert^2.$$ (5.4)

Other quantities such as total number density are likewise calculated as sums over all lattice points. By adding $n_k * number of points$ for all bins you can find the sum of $n_k$ over the whole lattice.